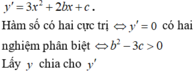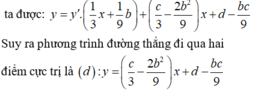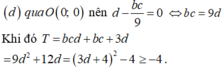Các câu hỏi tương tự
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình 3x – y + 9 0 và đường tròn (C) có phương trình:
x
2
+
y
2
+
2
x
−
6
y
+
6
0
.Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đườn...
Đọc tiếp
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình 3x – y + 9 = 0 và đường tròn (C) có phương trình: x 2 + y 2 + 2 x − 6 y + 6 = 0 .
Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đường tròn (C’) theo thứ tự là ảnh của M, d và (C) qua
a) Phép đối xứng qua gốc tọa độ;
b) Phép đối xứng qua tâm I.
Đồ thị hàm số
y
-
x
3
+
(
m
-
2
)
x
2
-
3
m
+
3
có hai điểm phân biệt đối xứng với nhau qua gốc tọa độ O khi giá trị của m là A. m 0 A. m 0 B. m -1 C. m 1, m 2 D. m -1, m 1
Đọc tiếp
Đồ thị hàm số y = - x 3 + ( m - 2 ) x 2 - 3 m + 3 có hai điểm phân biệt đối xứng với nhau qua gốc tọa độ O khi giá trị của m là A. m < 0
A. m < 0
B. m > -1
C. m < 1, m > 2
D. m < -1, m > 1
Đồ thị hàm số
y
-
x
3
+
(
m
-
2
)
x
2
-
3
m
+
3
có hai điểm phân biệt đối xứng với nhau qua gốc tọa độ O khi giá trị của...
Đọc tiếp
Đồ thị hàm số y = - x 3 + ( m - 2 ) x 2 - 3 m + 3 có hai điểm phân biệt đối xứng với nhau qua gốc tọa độ O khi giá trị của m là
A. m < 0
B. m > -1
C. m < 1, m > 2
D. m < -1, m > 1
Đồ thị hàm số
y
-
x
3
+
(
m
-
2
)
x
2
-
3
m
+
3
có hai điểm phân biệt đối xứng với nhau qua gốc tọa độ O khi giá trị của...
Đọc tiếp
Đồ thị hàm số y = - x 3 + ( m - 2 ) x 2 - 3 m + 3 có hai điểm phân biệt đối xứng với nhau qua gốc tọa độ O khi giá trị của m là
A. m < 0
B. m > -1
C. m < 1, m > 2
D. m < -1, m > 1
Biết
A
(
x
1
;
y
1
)
,
B
(
x
2
;
y
2
)
là hai điểm thuộc đồ thị (C) của hàm số
y
x
+
2...
Đọc tiếp
Biết A ( x 1 ; y 1 ) , B ( x 2 ; y 2 ) là hai điểm thuộc đồ thị (C) của hàm số y = x + 2 2 x - 1 cách đều hai điểm M(0;2), N(2;0). Giá trị biểu thức p = x 1 + x 2 - 2 x 1 x 2 bằng
![]()
![]()
![]()
![]()
Cho hàm số
y
x
4
-
2
m
x
2
+
1
-
m
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ O làm trực tâm. A. m 1 B. m 2 C. m 0 D. m -1
Đọc tiếp
Cho hàm số y = x 4 - 2 m x 2 + 1 - m . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ O làm trực tâm.
A. m = 1
B. m = 2
C. m = 0
D. m = -1
Biết rằng hàm số y sin2x + b.cosx - x ( 0 x
π
) đạt cực trị tại các điểm
x
π
6
và
x
π
2
Tính giá trị của biểu thức T a - b
Đọc tiếp
Biết rằng hàm số y = sin2x + b.cosx - x ( 0 < x < π ) đạt cực trị tại các điểm x = π 6 và x = π 2 Tính giá trị của biểu thức T = a - b
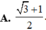
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
3
-
3
x
2
+
m
có hai điểm phân biệt đối xứng nhau qua gốc tọa độ. A.
m
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 - 3 x 2 + m có hai điểm phân biệt đối xứng nhau qua gốc tọa độ.
A. m > 1
B. m > 0
C. m ≤ 0
D. 0 < m < 1
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
3
-
3
x
2
+
m
có hai điểm phân biệt đối xứng nhau qua gốc tọa độ. A.
m
1
B. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 - 3 x 2 + m có hai điểm phân biệt đối xứng nhau qua gốc tọa độ.
A. m > 1
B. m > 0
C. m ≤ 0
D. 0 < m < 1