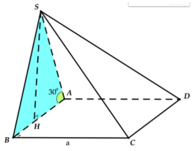
Dựng SH ⊥ AB, do (SAB) ⊥ (ABCD) ⇒ SH ⊥ (ABCD).
Ta có, do ΔSHA vuông tại H:
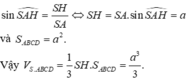

Dựng SH ⊥ AB, do (SAB) ⊥ (ABCD) ⇒ SH ⊥ (ABCD).
Ta có, do ΔSHA vuông tại H:
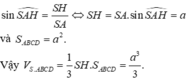
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), S A B ^ = 30°, SA = 2a. Tính thể tích V của khối chóp S.ABCD.
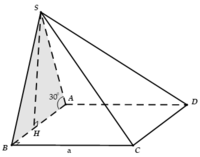
A. a 3 3 6
B. a 3 3
C. a 3 9
D. a 3
Cho hình chóp S.ACBD có đáy là hình vuông cạnh a mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), S A B ^ = 60°, SA = 2a Tính thể tích V của khối chóp S.ABCD
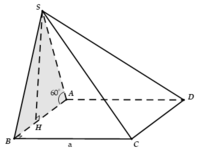
A. V = a 3 3 3
B. V = a 3 3
C. V = 2 a 3 3 3
D. V = a 3
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, SA = 2a . Tính theo a thể tích khối chóp S.ABCD.
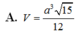
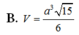
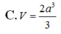
![]()
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy, S A = 2 a . Thể tích khối chóp S.ABCD theo a là:
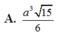
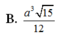

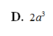
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng 60 0 . Tính thể tích V của khối chóp S.ABCD.
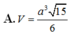
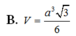
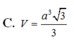
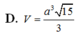
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên (SAB) là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng góc giữa mặt phẳng (SAD) và đáy bằng 450. Tính thể tích V của khối chóp S.ABCD.
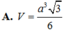
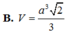
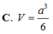
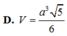
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết thể tích khối chóp S.ABCD bằng a 3 6 .
Độ dài cạnh bên SA bằng bao nhiêu?
A. SA = a
B. SA = a 2
C. SA = a 3 2
D. SA = a 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy, cạnh bên SC tạo với mặt phẳng (SAB) một góc 30°. Thể tích của khối chóp đó bằng:
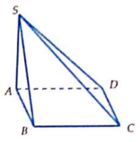
A. a 3 3 3
B. a 3 2 4
C. a 3 2 2
D. a 3 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của AB. Tính thể tích khối chóp S.ABCD.
A. a 3 3 6
B. a 3 3 3
C. a 3 3 12
D. a 3 3 2