Chọn A.
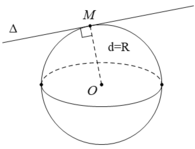
Đường thẳng Δ tiếp xúc với S( O; R) khi d = R.
Chọn A.

Đường thẳng Δ tiếp xúc với S( O; R) khi d = R.
Cho mặt cầu S(O;R) và đường thẳng Δ. Biết khoảng cách từ O tới Δ bằng d. Đường thẳng Δ tiếp xúc với S(O; R) khi thỏa mãn điều kiện nào trong các điều kiện sau ?
A. d = R.
B. d > R
C. d < R.
D. d ≠ R.
Cho mặt cầu S(O;R) và đường thẳng ∆ . Biết khoảng cách từ O tới ∆ bằng d. Với điều kiện nào sau đây thì đường thẳng ∆ tiếp xúc với mặt cầu S(O;R)?
A. d = R B. d > R
C. d < R D. d ≠ R
Trong không gian cho đường thẳng Δ và điểm O cách Δ một khoảng bằng 20cm. Mặt cầu (S) tâm O cắt đường thẳng Δ theo một dây có độ dài 30cm có bán kính r bằng:
A. r = 45cm
B. r = 30cm
C. r = 25cm
D. r = 20cm
Cho mặt cầu S(O;R) và điểm A cố định với OA = d > R. Qua A kẻ đường thẳng ∆ tiếp xúc với mặt cầu S(O;R) tại M. Độ dài đoạn thẳng AM là:
A. d 2 + R 2 B. 2 R 2 - d 2
C. R 2 - 2 d 2 D. d 2 - R 2
Cho mặt cầu S(O; R) và điểm A cố định với OA = d. Qua A, kẻ đường thẳng tiếp xúc với mặt cầu S(O; R) tại M. Công thức nào sau đây được dùng để tính độ dài đoạn thẳng AM?
A. 2 R 2 - d 2
B. d 2 - R 2
C. R 2 - 2 d 2
D. d 2 + R 2
Cho mặt cầu S(O;R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O;R) là đường tròn có bán kính bằng bao nhiêu?
A. R d
B. R 2 + d 2
C. R 2 - d 2
D. R 2 - 2 d 2
Cho mặt cầu S(O; R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O; R) là đường tròn có bán kính bằng bao nhiêu?
A. R d
B. R 2 + d 2
C. R 2 - d 2
D. R 2 - 2 d 2
Cho mặt cầu S(0;R) và mặt phẳng ( α ). Gọi d là khoảng cách từ O tới ( α ). Khi d < R thì mặt phẳng ( α ) cắt mặt cầu S(O;R) theo giao tuyến là đường tròn có bán kính bằng:
A. R 2 + d 2 B. R 2 - d 2
C. R d d. R 2 - 2 d 2
Cho mặt cầu (S) tâm O bán kính R và một đường thẳng d. Kí hiệu h là khoảng cách từ O đến đường thẳng d. Đường thẳng d có điểm chung với mặt cầu (S) nếu và chỉ nếu:
A. h ≤ R
B. h = R
C. h > R
D. h < R