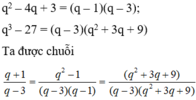Các câu hỏi tương tự
Tìm phân thức Q thỏa mãn đẳng thức sau:
Q
:
4
q
2
−
4
2
q
+
3
4
q
2
+
12
q
+
9...
Đọc tiếp
Tìm phân thức Q thỏa mãn đẳng thức sau: Q : 4 q 2 − 4 2 q + 3 = 4 q 2 + 12 q + 9 q − 1 với q ≠ − 3 2 và q ≠ 1
Phương pháp 2: dùng hằng đẳng thức
1) \(4x^2-y^2\)
2) \(8x^3-27\)
3) \(x^3+27y^3\)
4) \(x^2-25y^2\)
5) \(8x^3+\frac{1}{27}\)
q+1/q-3= .../q^2-4q+3= .../q^3-27 với q # 1 và q # 3
phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức 1) 8x^6-frac{1}{125}y^32) left(x+4right)^3-643)x^6+14)x^9+15)x^{12}-y^46)x^3+6x^2+12x+87) x^3-15x^2+75x-1258)27a^3-54a^2b+36ab^2-8b^3
Đọc tiếp
phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
1) \(8x^6-\frac{1}{125}y^3\)
2) \(\left(x+4\right)^3-64\)
3)\(x^6+1\)
4)\(x^9+1\)
5)\(x^{12}-y^4\)
6)\(x^3+6x^2+12x+8\)
7) \(x^3-15x^2+75x-125\)
8)\(27a^3-54a^2b+36ab^2-8b^3\)
phân tích đa thức thành nhân tử
\(x^3+2x^2+2x+1\)
\(x^3-4x^2+12x-27\)
\(x^4+2x^3+2x^2+2x+1\)
\(x^4-2x^3+2x-1\)
trong hằng đẳng thức \(\left(x+1\right)^3=x^3+3x^2+3x+1\) lần lượt thay x bằng giá trị \(1;2;3;4;....;n\) vào hằng đẳng thức, rồi cộng các đẳng thức lại, bằng cách đó hãy tính :
\(S=1^3+2^3+3^3+n^3\) từ hẳng đẳng thức \(\left(x+1\right)^4=x^4+4x^3+6x^2+4x+1\)
phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức:
a)1+\(8x^6y^3\)
b)\(x^3+6x^2+12x+8\)
c)\(x^3+\frac{3}{2}x^2+\frac{3}{4}x+\frac{1}{8}\)
d)\(27x^3-54x^2y+36xy^2-8y^3\)
e)\(1-9x+27x^2-27x^3\)
Viết các đa thức sau thành tích:
\(16-x^2\)
\(4x^2-9\)
\(a^4-25\)
\(\left(a+b\right)^2-1\)
\(\left(a+b\right)^2-\left(m-n\right)^2\)
\(x^3-27\)
\(64x^3+\frac{1}{27}\)
Hoàn thành chuỗi đẳng thức sau:
(
m
−
2
)
(
.
..
)
2
m
2
−
m
−
3
.
..
4...
Đọc tiếp
Hoàn thành chuỗi đẳng thức sau: ( m − 2 ) ( . .. ) 2 m 2 − m − 3 = . .. 4 m 2 − 9 = . .. 8 m 3 − 27 với m ≠ − 1 và m ≠ ± 3 2 .