Các câu hỏi tương tự
Hình hộp chữ nhật ABCD.ABCD có AC
3
a; AB 2a; AD
5
a (a 0). Tính thể tích tứ diện ABDA. A. V
a
3
6
B. V
a
3
15
3
C. V
a
3
2
3...
Đọc tiếp
Hình hộp chữ nhật ABCD.A'B'C'D' có AC = 3 a; AB' = 2a; AD' = 5 a (a > 0). Tính thể tích tứ diện ABDA'.
A. V = a 3 6
B. V = a 3 15 3
C. V = a 3 2 3
D. V = a 3 3
Cho hình hộp chữ nhật ABCD.ABCD có AB a, AA - 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD là
9
π
2
a
3
. Tính thể tích V của hình chữ nhật A.
2
a
3
3
B.
2
a
3
C.
4...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA - 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π 2 a 3 .
Tính thể tích V của hình chữ nhật
A. 2 a 3 3
B. 2 a 3
C. 4 a 3
D. 4 a 3 3
Cho khối hộp chữ nhật ABCD.ABCD có
A
B
a
,
A
D
b
,
A
C
c
. Thể tích khối hộp chữ nhật ABCD.ABCD bằng bao nhiêu?
Đọc tiếp
Cho khối hộp chữ nhật ABCD.A'B'C'D' có A B = a , A D = b , A C = c . Thể tích khối hộp chữ nhật ABCD.A'B'C'D' bằng bao nhiêu?
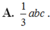
![]()
![]()
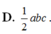
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khi đó thể tích hình chóp A.A'BCD' bằng:
A. a 3 /2 B. a 3 /3
C. a 3 /4 D. a 3 /6
Cho hình hộp ABCD.ABCD có đáy là hình chữ nhật, hình chiếu của A lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB a, AD 2a và thể tích hình hộp đã cho bằng 2
a
3
. Khoảng cách từ B đến mặt phẳng (ADCB) bằng:A.
2
a
6
B.
2...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
Cho hình hộp chữ nhật ABCD.ABCD có AB1, BC2, AA3. Mặt phẳng (P) thay đổi và luôn đi qua C’, mặt phẳng (P) cắt các tia AB, AD, AA’ lần lượt tại E, F, G (khác A). Tính tổng TAE+AF+AG sao cho thể tích khối tứ diện AEFG nhỏ nhất. A. 15 B. 16 C. 17 D. 18
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=1, BC=2, AA'=3. Mặt phẳng (P) thay đổi và luôn đi qua C’, mặt phẳng (P) cắt các tia AB, AD, AA’ lần lượt tại E, F, G (khác A). Tính tổng T=AE+AF+AG sao cho thể tích khối tứ diện AEFG nhỏ nhất.
A. 15
B. 16
C. 17
D. 18
Cho hình hộp chữ nhật ABCD.ABCD có AB a, AD 2a, AC
6
a. Thể tích khối hộp chữ nhật ABCD.ABCD bằng: A.
3
a
3
3
B.
2
a
3
3
C.
2
a
3
D.
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = 2a, AC' = 6 a. Thể tích khối hộp chữ nhật ABCD.A'B'C'D' bằng:
A. 3 a 3 3
B. 2 a 3 3
C. 2 a 3
D. 2 3 a 3
Cho hình hộp chữ nhật ABCD.ABCD, biết AB 2AD và tổng diện tích 6 mặt bằng 12, thì hình hộp có thể tích lớn nhất (
V
m
a
x
) bằng bao nhiêu? A.
V
m
a
x
8
3
B.
V
m
a
x
...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D', biết AB = 2AD và tổng diện tích 6 mặt bằng 12, thì hình hộp có thể tích lớn nhất ( V m a x ) bằng bao nhiêu?
A. V m a x = 8 3
B. V m a x = 2 2
C. V m a x = 3
D. V m a x = 10 3
Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A' trên cạnh SA sao cho SA' = SA/3. Mặt phẳng qua A' và song song với đáy của hình chóp cắt cạnh SB, SC, SD lần lượt tại B', C', D'. Thể tích hình chóp S.A'B'C'D' bằng:
A. V/3 B. V/9
C. V/27 D. V/81.



