Các câu hỏi tương tự
Cho hình chữ nhật ABCD cạnh AB 4, AD 2. Gọi M,N lần lượt là trung điểm AB và CD. Cho hình chữ nhật quay quanh MN ta thu được hình trụ tròn xoay. Tính thể tích của hình trụ tròn xoay. A.
V
4
π
B.
V
8
π
C.
V
16
π
D.
V
...
Đọc tiếp
Cho hình chữ nhật ABCD cạnh AB = 4, AD = 2. Gọi M,N lần lượt là trung điểm AB và CD. Cho hình chữ nhật quay quanh MN ta thu được hình trụ tròn xoay. Tính thể tích của hình trụ tròn xoay.
A. V = 4 π
B. V = 8 π
C. V = 16 π
D. V = 32 π
Hình chữ nhật ABCD có AB4, AD2. Gọi M và N lần lượt là trung điểm của AB và CD. Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng
Đọc tiếp
Hình chữ nhật ABCD có AB=4, AD=2. Gọi M và N lần lượt là trung điểm của AB và CD. Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng
![]()
![]()
![]()
![]()
Cho hình chữ nhật ABCD có AB2AD và M, N lần lượt là trung điểm của các cạnh AB và CD. Khi quay hình chữ nhật ABCD quanh đường thẳng MN ta được một khối tròn xoay có thể tích bằng
8
πa
3
. Diện tích của hình chữ nhật ABCD là A.
2
a
2
B.
16
a
2
C.
8
a
2...
Đọc tiếp
Cho hình chữ nhật ABCD có AB=2AD và M, N lần lượt là trung điểm của các cạnh AB và CD. Khi quay hình chữ nhật ABCD quanh đường thẳng MN ta được một khối tròn xoay có thể tích bằng 8 πa 3 . Diện tích của hình chữ nhật ABCD là
A. 2 a 2
B. 16 a 2
C. 8 a 2
D. 4 a 2
Cho hình chữ nhật ABCD có ABa, BC2a. Gọi M,N lần lượt là trung điểm của AB và CD. Thể tích của khối trụ tạo thành khi quay hình chữ nhật ABCD quanh trục MN bằng
Đọc tiếp
Cho hình chữ nhật ABCD có AB=a,
BC=2a. Gọi M,N lần lượt là trung điểm
của AB và CD. Thể tích của khối trụ tạo
thành khi quay hình chữ nhật ABCD
quanh trục MN bằng
![]()
![]()
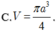
![]()
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết AB 4,AD 7. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
Đọc tiếp
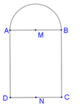
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết AB = 4,AD = 7. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
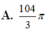
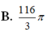
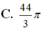
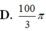
Cho hình chữ nhật ABCD có cạnh AB
4
3
, AD 1. Lấy điểm M trên CD sao cho MD
3
. Cho hình vẽ quay quanh AB, tam giác MAB tạo thành vật tròn xoay gồm 2 hình nón chung đáy. Tính diện tích toàn phần của vật tròn xoay này.
Đọc tiếp
Cho hình chữ nhật ABCD có cạnh AB = 4 3 , AD = 1. Lấy điểm M trên CD sao cho MD = 3 . Cho hình vẽ quay quanh AB, tam giác MAB tạo thành vật tròn xoay gồm 2 hình nón chung đáy. Tính diện tích toàn phần của vật tròn xoay này.
![]()

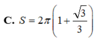
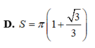
Cho hình chữ nhật ABCD có ABa, BC2a. Trên tia đối của tia AB lấy điểm O sao cho OAx. Gọi d là đường thẳng đi qua O và song song với AD. Tìm x biết thể tích của khối tròn xoay tạo nên khi quay hình chữ nhật ABCD quanh d gấp ba lần thể tích khối cầu có bán kính bằng cạnh AB.
Đọc tiếp
Cho hình chữ nhật ABCD có AB=a, BC=2a. Trên tia đối của tia AB lấy điểm O sao cho OA=x. Gọi d là đường thẳng đi qua O và song song với AD. Tìm x biết thể tích của khối tròn xoay tạo nên khi quay hình chữ nhật ABCD quanh d gấp ba lần thể tích khối cầu có bán kính bằng cạnh AB.
![]()
![]()
![]()
![]()
Trong không gian, cho hình chữ nhật ABCD có AB1 và AD2. Gọi M, N lần lượt là trung điểm của AB và CD. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính thể tích V của khối trụ tạo bởi hình trụ đó. A.
π
2
B.
π
C.
2
π
D. 4
π
Đọc tiếp
Trong không gian, cho hình chữ nhật ABCD có AB=1 và AD=2. Gọi M, N lần lượt là trung điểm của AB và CD. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính thể tích V của khối trụ tạo bởi hình trụ đó.
A. π 2
B. π
C. 2 π
D. 4 π
Cho hình chữ nhật ABCD, AB a, góc giữa AC,BD bằng
60
o
(ABBC). Cho hình chữ nhật ABCD quay quanh AB tạo thành một khối tròn xoay có thể tích V. Tính V.
Đọc tiếp
Cho hình chữ nhật ABCD, AB = a, góc giữa AC,BD bằng 60 o (AB<BC). Cho hình chữ nhật ABCD quay quanh AB tạo thành một khối tròn xoay có thể tích V. Tính V.
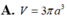
![]()
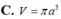
![]()




