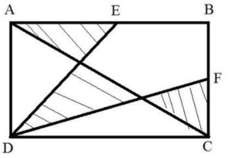
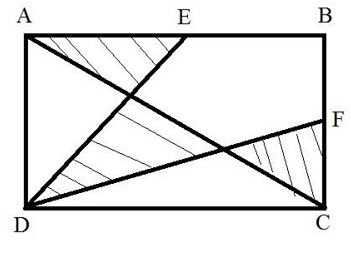
Gọi I, K lần lượt là giao điểm của AC với ED và DF với AC. Gọi a,b là chiều dài, chiều rộng của hình chữ nhật. Kẻ EN, DM vuông góc với AC (N, M thuộc AC).
Ta có diện tích tam giác AED bằng ¼ ab, diện tíchtam giác FCD bằng ¼ ab, suy ra diện tích tứ giác EBFD bằng ½ ab. (*)
Ta lại có, SABC =SAEI + SEBFKI + SFKC = ½ AB (**)
Từ (*) và (**) suy ra SDIK = SAEI + SFKC
Lập luận tương tự ta suy ra SEBFKI = SAID + SCKD.
Từ đó suy ra 2(SAEI + SFKC) + 2(SAID + SCKD)= SABCD (tức là bằng a/b) (1)
DM là đường cao trong tam giác vuông ACD nên (1/DM)2=(1/a)2+(1/b)2
Tương dương DM= (ab)2/(a2+b2).
Gọi O là trung điểm của AC.
Ta có tam giác EDO đồng dạng tam giấcEO(g,g,g)
Suy ra EN/AE = EO/AO =(1/2b)/(1/2AC)=b/AC
Tương đương EN=b×AE/AC= (b×1/2a)/AC =
ab/2 a 2 + b 2
Từ đó, ta có SAID = ½ DM×AI= ½(ab)2/(a2+b2)×AI.
Suy ra SAID/SAEI= 2ab/2 a 2 + b 2
Làm tương tự để xác định tỉ số SDKC/SBKC
Sau đó rút ra gia trị của tổng diện tích các tam giác(phân gạch chéo)