Question

Hình chóp S.ABC là hình chóp tam giác đều, có cạnh đáy bằng a và cạnh bên bằng a 2 . Một mặt cầu đi qua đỉnh A và tiếp xúc với hai cạnh SB , SC tại trung điểm của mỗi cạnh. Chứng minh rằng mặt cầu đó đi qua trung điểm của AB và AC.

Answer 1

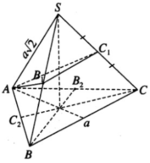
Giả sử mặt cầu đi qua đỉnh A của hình chóp và tiếp xúc với cạnh SB tại B1, tiếp xúc với cạnh SC tại C 1 . Khi đó mặt cầu cắt cạnh AB, AC lần lượt tại các điểm C 2 ,   B 2 . Mặt phẳng (SAB) cắt mặt cầu đó theo giao tuyến là một đường tròn. Đường tròn này tiếp xúc với SB tại B1 và đi qua A và  C 2

Do đó, ta có: BB 1 2 = BA . BC 2

trong đó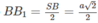 

Do đó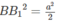 

Vậy

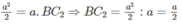
Điều đó chứng tỏ mặt cầu nói trên đi qua trung điểm  C 2  của đoạn AB. Lí luận tương tự ta chứng minh được mặt cầu đó đi qua trung điểm  B 2  của AC.