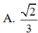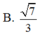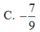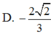Chọn D.
Gọi O là giao điểm của BC và AD.
Khi quay hình ABCD quanh BC tức là quay tam giác vuông OBA quanh OB và quay tam giác vuông OCD quanh OC. Mỗi hình quay sẽ tạo ra một hình nón nên hình tạo ra sẽ tạo ra 2 hình nón.
Cho tứ diện đều ABCD. Khi quay tứ diện đó xung quanh trục là AB có bao nhiêu hình nón khác nhau được tạo thành?
A. Một B. Hai
C. Ba D. Không có hình nón nào
Cho tứ diện ABCD có AD ⊥ (ABC) và BD ⊥ BC. Khi quay tứ diện đó xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
A. Một B. Hai
C. Ba D. Bốn
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy SC = a 6 . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:
A. 4 πa 3 3
B. πa 3 2 6
C. πa 3 3 3
D. πa 3 6 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy S C = a 6 . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:
A. 4 πa 3 3
B. a 3 π 2 6
C. πa 3 3 3
D. πa 3 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy S C = a 6 . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:
A. 4 πa 3 3
B. a 3 π 2 6
C. π a 3 3 3
D. π a 3 3 6
Tam giác ABC vuông đỉnh A có AB = 2AC. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo ra hình nón (N1) và quay tam giác ABC quanh trục AC thì đoạn gấp khúc ABC tạo ra hình nón (N2). Tỉ số diện tích xung quanh của hình nón (N1) và diện tích xung quanh của hình nón (N2) là:
A. 1/4
B. 1/2
C. 1
D. 2
Cho hình nón (N) có bán kính đáy r=20(cm), chiều cao h=60(cm) và một hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
Một hình nón có góc ở đỉnh bằng 90°. Hình trụ có chung trục với hình nón. Một đáy của nó thuộc mặt đáy hình nón, đáy còn lại thuộc mặt xung quanh hình nón có bán kính bằng 2 3 bán kính đường tròn đáy hình nón. Tính k = V T V N (VT, VN là thể tích hình trụ, hình nón).
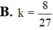
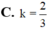
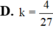
Một hình trụ có hai đáy là hai hình tròn (O;r) và (O';r). Khoảng cách giữa hai đáy là O O ' = r 3 . Một hình nón có đỉnh là O’ và có đáy là hình tròn (O;r). Mặt xung quanh của hình nón chia khối trụ thành 2 phần. Gọi V 1 là thể tích phần bên ngoài khối nón, V 2 là phần thể tích bên trong khối nón. Khi đó V 1 V 2 bằng:
A. 1 2
B. 1 3
C. 2
D. 3
Cho hình trụ T. Một hình nón N có đáy là một đáy của hình trụ, đỉnh S của hình nón là tâm của đáy còn lại. Biết tỉ số diện tích xung quanh của hình nón và diện tích xung quanh của hình trụ bằng 3 2 .Gọi β là góc ở đỉnh của hình nón đã cho. Tính cos β
