Bài 9:
\(a,75.20,9+5^2.20,9=20,9\left(75+25\right)=25,9.100=2590\)
\(b,86.15+150.1,4=86.15+15.10.1,4=86.15+15.14=15\left(86+14\right)=15.100=1500\)
\(c,93.32+14.16=93.2.16+14.16=186.16+14.16=16\left(186+14\right)=16.200=3200\)
\(d,98,6.199-990.9,86=98,6.199-99.10.9,86=98,6.199-99.98,6=98,6\left(199-99\right)=98,6.100=9860\)
Bài 10:
\(a,A=a\left(b+2\right)+b\left(2+b\right)\) tại \(a=2\) và \(b=3\)
\(=a\left(b+2\right)+b\left(b+2\right)\)
\(=\left(b+2\right)\left(a+b\right)\)
Thay a = 2 ; b = 3 vào biểu thức ta được:
\(\left(3+2\right)\left(2+3\right)=5.5=25\)
Vậy giá trị của biểu thức A = 25 tại a = 2; b = 3
_______________________________________
\(b,B=b^2+b+c\left(b+1\right)\) tại b = 1 và c = 2
\(=b\left(b+1\right)+c\left(b+1\right)\)
\(=\left(b+c\right)\left(b+1\right)\)
Thay ....... ta được: \(\left(1+2\right)\left(1+1\right)=3.2=6\)
Vậy .........
_______________________________________
\(c,C=xy\left(x-y\right)-2y+2y\) tại xy = 8 và x - y = 5
\(=xy\left(x-y\right)-2\left(x-y\right)\)
\(=\left(x-y\right)\left(xy-2\right)\)
Thay ........ ta được: \(5\left(8-2\right)=5.6=30\)
Vậy .........
_______________________________________
\(d,D=x\left(x+y\right)-xy\left(x+y\right)\) tại x = 1 và y = -5
\(=\left(x+y\right)\left(x-xy\right)\)
Thay ........ ta được: \(\left[1+\left(-5\right)\right]\left[1-\left(-5.1\right)\right]=-4.6=-24\)
Vậy .........
Bài 11:
\(a,x\left(x-3\right)-2x+6=0\)
\(\Rightarrow x\left(x-3\right)-2\left(x-3\right)=0\)
\(\Rightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
Vậy \(x\in\left\{2;3\right\}\)
__________________________
\(b,\dfrac{x}{3}+\dfrac{x^2}{2}=0\)
\(\Rightarrow\dfrac{x.2}{6}+\dfrac{x^2.3}{6}=\dfrac{0}{6}\)
\(\Rightarrow x.2+x^2.3=0\)
\(\Rightarrow x\left(1.2+x.3\right)=0\)
\(\Rightarrow x\left(2+3x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\2+3x=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{2}{3}\end{matrix}\right.\)
Vậy \(x\in\left\{0;\dfrac{-2}{3}\right\}\)






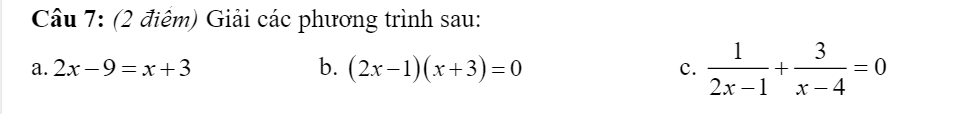 help mik
help mik
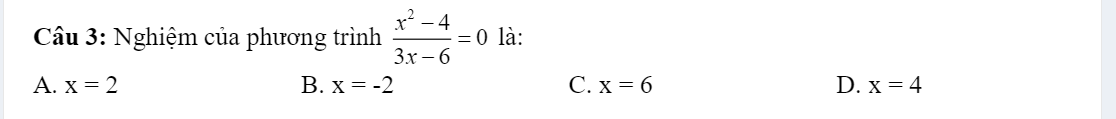
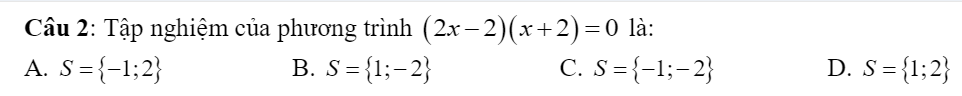
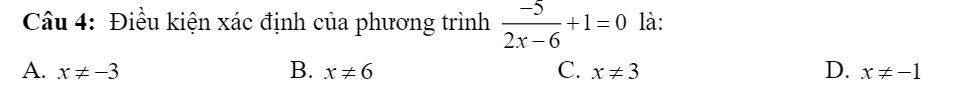
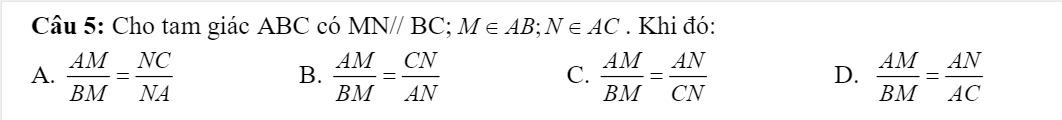 help mik vs
help mik vs 





 help mik vs mai phải nộp r;-;
help mik vs mai phải nộp r;-;


