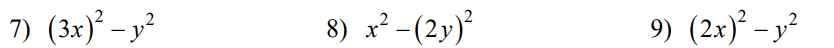Các hàng đẳng thức lớp 7 đc học là ;
\(\left(a+b\right)^2=a^2+2ab+b^2\)
\(\left(a-b\right)^2=a^2-2ab+b^2\)
\(a^2-b^2=\left(a+b\right).\left(a-b\right)\)
Vì câu hỏi ghi toán 7 nên chỉ có thế thôi chưa học đâu
7 hằng đẳng thức đáng nhớ là :
\(\left(a+b\right)^2=a^2+2ab+b^2\)
\(\left(a-b\right)^2=a^2-2ab+b^2\)
\(a^2-b^2=\left(a+b\right)\left(a-b\right)\)
\(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
\(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
\(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)
\(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)
~ Hok tốt ~
1.Bình phương của 1 tổng bằng bình phương số thứ 1 cộng hai lần tích của số thứ nhất với số thứ hai cộng bình phương số thứ hai
2.Bình phương của 1 hiệu bằng bình phương số thứ 1 trừ 2 lần tích số thứ nhất với số thứ 2 cộng với bình phương số thứ 2.
3.Hiệu 2 bình phương bằng tích của tổng 2 số với hiệu 2 số.
4.Lập phương của 1 tổng bằng lập phương số thứ 1 + 3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 + lập phương số thứ 2.
5. Lập phương của 1 tổng bằng lập phương số thứ 1 -3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 - lập phương số thứ 2.
6.Tổng hai lập phương bằng tích giữa tổng 2 số với bình phương thiếu của 1 hiệu.
7.Hiệu 2 lập phương bằng tích giữa hiệu hai số với bình phương thiếu của 1 tổng.
Lên wiki tìm có hết nhé
\(\left(a+b\right)^2=a^2+2ab+b^2\)
\(\left(a-b\right)^2=a^2-2ab+b^2\)
\(a^2-b^2=\left(a+b\right)\left(a-b\right)\)
\(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)
\(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)
\(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
\(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)