Chọn A.
Hàm số 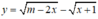 có nghĩa khi và chỉ khi:
có nghĩa khi và chỉ khi:
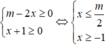
Để tập xác định của hàm số là một đoạn thì 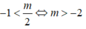
Chọn A.
Hàm số 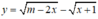 có nghĩa khi và chỉ khi:
có nghĩa khi và chỉ khi:
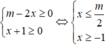
Để tập xác định của hàm số là một đoạn thì 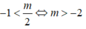
Tìm tất cả các giá trị của tham số m để tập xác định của hàm số
y = m x - 2 - x + 1 là một đoạn trên trục số.
A. m<-2
B. m>-2
C. m>2
D. m<2
Tập xác định của hàm số y = x - m - 6 - 2 x là một đoạn trên trục số khi và chỉ khi:
A. m < 3
B. m = 3
C. m > 3
D. m < 1 3
y= \(\dfrac{mx}{\sqrt{x-m+2}+1}\)
a, Tìm tập xác định của hàm số theo tham số m
b, Tìm m để hàm số có tập xác định trên (0;1)
Câu 1.
a) Cho tập A,B lần lượt là tập xác định của hàm số f(x) = \(\sqrt{6-x}\) và g(x) = \(\dfrac{3}{2x+1}\). Xác định các tập A∩B, A∪B, A∖B, CRA.
b) Cho tập hợp C=[−3;8] và D=[m−6;m+3). Với giá trị nào của m thì C∩D là một đoạn thẳng có độ dài bằng 4.
định m để hàm số y = \(\sqrt{\left(m-2\right)x^2+\left(m-2\right)x+4}\) có tập xác định là R?
A. 2 ≤ m ≤ 18 B. \(\left\{{}\begin{matrix}m< 2\\m>18\end{matrix}\right.\) C.\(\left\{{}\begin{matrix}m\le2\\m\ge18\end{matrix}\right.\) D.-2<m<18
Hàm số \(\dfrac{x+2}{x-m+2}\) xác định trên (1; 3) khi:
A. m < 3 B. m ≥5 C. m < 3 hoặc m > 5 D. m ≥ 5 hoặc m ≤ 3.
Cho hàm số y = f(x) = mx + 2m − 3 có đồ thị (d). gọi A, B là hai điểm thuộc đồ thị
và có hoành độ lần lượt là −1 và 2.
1 Xác định tọa độ hai điểm A và B.
2 Tìm m để cả hai điểm A và B cùng nằm phía trên trục hoành.
3 Tìm điều kiện của m để f(x) > 0, ∀x ∈ [−1; 2]
Cho hàm số y=x²-mx-3(1) a/Tìm m để đồ thị hàm số (1) cắt Õ tại điểm có hoành độ bằng 3 b/lập bảng biến thiên và vẽ đồ thị khi m=-2 c/Tìm tọa độ giao điểm (P) với đường thẳng (d)y=2x+9 d/tìm m để parabol của hàm số có đỉnh nằm trên trục Ox
Cho hàm số y = \(\frac{x^2-mx+m}{x-m}\). Hãy xác định m sao cho:
a) Đồ thị của hàm số không cắt trục tung
b) Đồ thị của hàm số không cắt trục hoành
c) Đồ thị của hàm số cắt trục hoành tại 2 điểm phân biệt