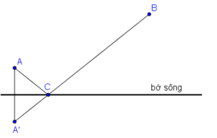
Gọi đường thẳng xy là bờ sông cần xây trạm bơm.
⇒ Bài toán đưa về: Hai điểm A, B cố định cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy. Tìm vị trí điểm C nằm trên đường xy sao cho CA + CB nhỏ nhất.
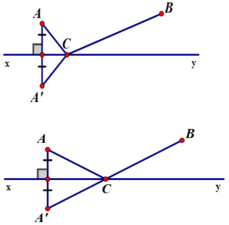
Gọi A’ là điểm đối xứng của A qua đường thẳng xy.
Theo như chứng minh ở bài 48 ta có: CA + CB = CA’ + CB ≥ A’B (A’B cố định).
⇒ CA + CB đạt ngắn nhất bằng A’B.
Dấu “=” xảy ra khi CA’+CB = A’B, tức là A’; B; C thẳng hàng hay C là giao điểm của A’B và xy.
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng A’B, trong đó A’ là điểm đối xứng với A qua xy.