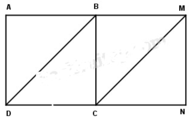
Cách 1:
Vì tứ giác ABCD, BMNC đều là hình vuông mà tứ giác BNMC là hình bình hàng suy ra đường cao h cũng chính là cạnh BC và độ dài đáy cũng chính là cạnh DC.
Diện tích hình bình hành BMCD là:
S = a x h = DC x BC = 3 x 3 = 9 (cm2)
Đáp số: 9cm2
Cách 2: Diện tích hình bình hành BMCD bằng diện tích tam giác BCD cộng với diện tích tam giác BCM.
Tam giác BCD có đường cao BC = 3cm, cạnh đá DC = 3cm
Diện tích tam giác BCD là:
SBCD = độ dài đáy x đường cao : 2
= DC x BC : 2 = 3 x 3 : 2 = 4,5 cm2
Tam giác BCM có đường cao CB = 3cm, cạnh đáy BM = 3cm
Diện tích tam giác BCM là:
SBCM = độ dài đáy x đường cao : 2
= CB x BM : 2 = 3 x 3 : 2 = 4,5 cm2
Diện tích hình bình hành BMCD là:
S = SBCD + SBCM = 4,5 + 4,5 = 9 cm2
Cách 3:
Diện tích hình bình hành BMCD bằng diện tích nửa hình vuông ABCD + diện tích nửa hình vuông BMNC.
Diện tích nửa hình vuông ABCD có cạnh bằng 3cm là:
3 x 3 : 2 = 4,5 cm2
Diện tích nửa hình vuông BMNC có cạnh bằng 3cm là:
3 x 3 : 2 = 4,5 cm2
Diện tích hình bình hành BMCD là:
S = 4,5 + 4,5 = 9 cm2