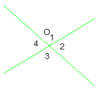
Giải: a) Ta có: \(\widehat{O_1}=\widehat{O_3}\) (đối đỉnh)
mà \(\widehat{O_1}+\widehat{O_3}=140^0\)
=> \(\widehat{O_1}=\widehat{O_3}=70^0\)
Ta lại có: \(\widehat{O_1}+\widehat{O_2}=180^0\)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-70^0=110^0\)
=> \(\widehat{O_2}=\widehat{O_4}=110^0\) (đối đỉnh)
b) Ta có: \(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=240^0\)
mà \(\widehat{O_1}+\widehat{O_2}=180^0\)(kề bù)
=> \(\widehat{O_3}=240^0-\left(\widehat{O_1}+\widehat{O_2}\right)=240^0-180^0=60^0\)
=> \(\widehat{O_3}=\widehat{O_1}=60^0\) (đối đỉnh)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-60^0=120^0\)
=> \(\widehat{O_2}=\widehat{O_4}=120^0\) (đối đỉnh)
c) Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\) (kề bù)
mà \(\widehat{O_2}-\widehat{O_1}=30^0\)
=> \(2.\widehat{O_2}=180^0+30^0=210^0\)
=> \(\widehat{O_2}=210^0:2=105^0\) => \(\widehat{O_2}=\widehat{O_4}=105^0\)(đối đỉnh)
=> \(\widehat{O_1}=180^0-105^0=75^0\) => \(\widehat{O_1}=\widehat{O_3}=75^0\) (đối đỉnh)
d) Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\) (kề bù)
=> \(\widehat{O_1}+2.\widehat{O_1}=180^0\)
=> \(3.\widehat{O_1}=180^0\)
=> \(\widehat{O_1}=180^0:3=60^0\) => \(\widehat{O_1}=\widehat{O_3}=60^0\) (đối đỉnh)
=> \(\widehat{O_2}=180^0-60^0=120^0\) => \(\widehat{O_2}=\widehat{O_4}=120^0\) (Đối đỉnh)
e) Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\) (kề bù)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-75^0=105^0\)
=> \(\widehat{O_2}=\widehat{O_4}=105^0\) (đối đỉnh)
Ta lại có: \(\widehat{O_1}=\widehat{O_3}\) (đối đỉnh)
Mà \(\widehat{O_1}=75^0\) => \(\widehat{O_3}=75^0\)