Question

(Hà Nội - 2020)

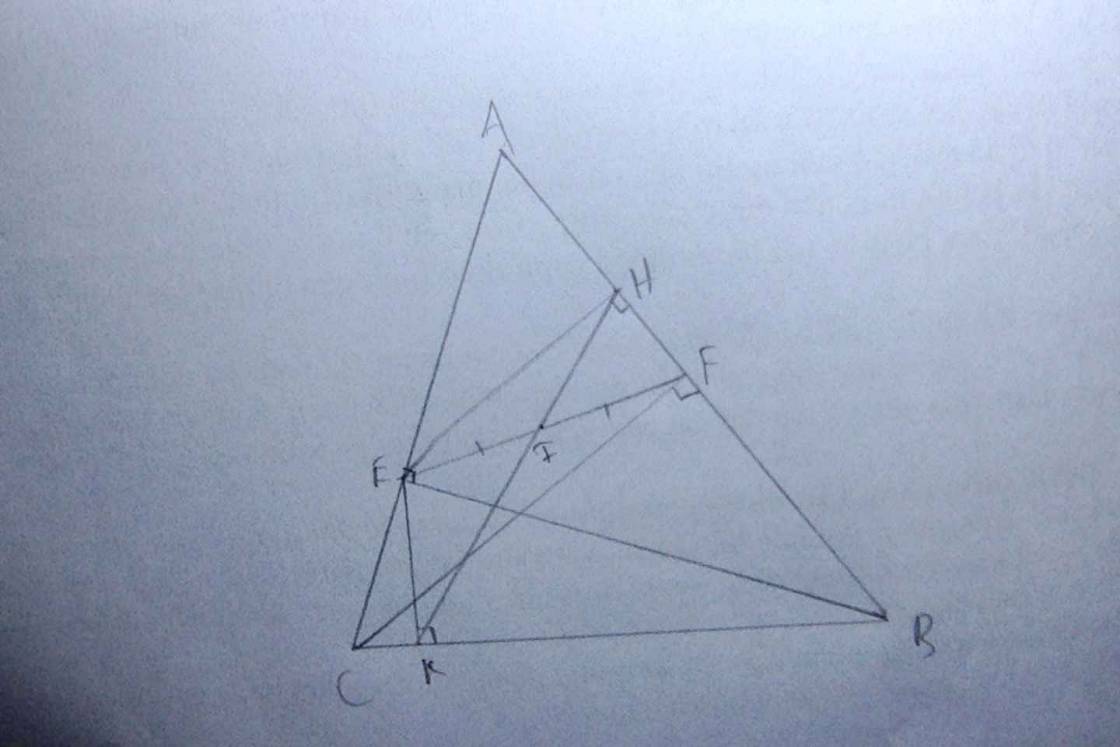
Cho tam giác $ABC$ có ba góc nhọn và đường cao $BE$. Gọi $H$ và $K$ lần lượt là chân các đường vuông góc kẻ từ điểm $E$ đến các đường thẳng $AB$ và $BC$.

1. Chứng minh tứ giác $BHEK$ là tứ giác nội tiếp.

2. Chứng minh $BH.BA = BK.BC$.

3. Gọi $F$ là chân đường vuông góc kẻ từ điểm $C$ đến đường thẳng $AB$ và $I$ là trung điểm của đoạn thẳng $EF$. Chứng minh ba điểm $H, I , K$ thẳng hàng.

Answer 1

Answer 2

Answer 3

Answer 4

Answer 5

FDGH

Answer 6

1 xét tg BHEK ta có góc BHE=góc BKE(=90) suy ra góc BHE+ góc BKE=180 và hai góc đối nhau 

Do đó tg BHEK là tgnt

2 xét tam giác ABE , góc BEA =90

ta có:BE²=BH.AB( hệ thức 1)   (1)

xét tam giác CBE, góc BEC=90

ta có : BE²=BK.BC=( hệ thức 1)    (2)

Từ (1) và (2) suy ra BH.AB=BK.BC 

3 Em không làm được ạ 

Answer 7

Chứng minh được \widehat{BHE} = 90^{\circ}BHE=90∘ và \widehat{BKE} = 90^{\circ}BKE=90∘.

Suy ra \widehat{BHE} + \widehat{BKE} = 180^{\circ}BHE+BKE=180∘.

Vậy tứ giác $BHEK$ là tứ giác nội tiếp.

2.

Áp dụng hệ thức lượng cho $\Delta AEB$ vuông tại $E$, đường cao $EH$ có: BH.BA = BE^2BH.BA=BE2.

Chứng minh tương tự ta có: BK.BC = BE^2BK.BC=BE2.

Vậy $BH.BA=BK.BC$.

3.

Chứng minh được:

\widehat{BHK} = \widehat{BEK}BHK=BEK (1) ($BHEK$ nội tiếp);

\widehat{BEK} = \widehat{BCE}BEK=BCE (2) (cùng phụ với \widehat{EBC}EBC);

\widehat{BCE} = \widehat{HFE}BCE=HFE (3) ($BCEF$ nội tiếp);

\widehat{HFE} = \widehat{FHI}HFE=FHI (4) (tam giác $FHI$ cân tại $I$).

Từ (1), (2), (3) và (4) suy ra \widehat{BHK} = \widehat{FHI}BHK=FHI. Do $\Delta ABC$ nhọn nên hai điểm $I$ và $K$ nằm cùng phía với đường thẳng $HF$ nên ba điểm $H,I,K$ thẳng hàng.

Answer 8

chưng minh được : BHE=90 độ và BKE=90 độ

suy ra BHE + BKE = 180 độ

vậy tứ giác BHEK là tứ giác nội tiếp

Answer 9

.                                    1.    có HE vuông góc với AB tại H ( giả thiết) 
=>góc EHB = 90^o 
có EK vuông góc với CB tại K ( giả thiết) ⇒góc EKB = 90⁰    

có góc EHB + góc EKB = 90 + 90 = 180^0.    
mà hai góc này nằm vị trí đối nhau  
=> tứ giác EHBK  nội tiếp ( dấu hiệu nhận biết tứ giác nội tiếp )

2. có BE vuông góc với AC tại E ( giả thiết) 

=> góc BEC = góc BEA = 90^o

=> tam giác BEC vuông tại E ,tam giác BEA vuông tại E 

mà có EK là đường cao tam giác BEC ,EH là đường cao tam giác BEA 

=> BH.BA =EB²      , BK.BC=EB^2.      

=> BK.BC=BH.BA ( cùng bằng EB ² )

3
 

 

Answer 10

1,Xét Δ ABC,có

EH vuông góc AB   giả thiết

⇒ góc BEH bằng 90 độ

EK vuông góc BC   giả thiết

⇒ góc EKB bằng 90 độ

Xét tứ giác BHEK,có

góc BEH cộng góc EKB

bằng 90 độ cộng 90 độ

bằng 180 độ

⇒ tg BHEK nội tiếp     định lý tg nội tiếp

2,Xét Δ EAB vg tại E,có

EH là đg cao

⇒BH.BA bằng BE bình             1

Xét Δ EBC vg tại E,có

EK là đg cao

⇒BK.BC bằng BE bình             2

Từ 1 và 2 ⇒BH.BC bằng BK.BC  đpcm

Answer 11

cuts

Answer 12

1.

Chứng minh được $\widehat{BHE}={90}^{\circ }$ và $\widehat{BKE}={90}^{\circ }$.

Suy ra $\widehat{BHE}+\widehat{BKE}={180}^{\circ }$.

Vậy tứ giác $BHEK$ là tứ giác nội tiếp.

2.

Áp dụng hệ thức lượng cho $\Delta AEB$ vuông tại $E$, đường cao $EH$ có: $BH.BA=B{E}^2$.

Chứng minh tương tự ta có: $BK.BC=B{E}^2$.

Vậy $BH.BA=BK.BC$.

3.

Chứng minh được:

$\widehat{BHK}=\widehat{BEK}$ (1) ($BHEK$ nội tiếp);

$\widehat{BEK}=\widehat{BCE}$ (2) (cùng phụ với $\widehat{EBC}$);

$\widehat{BCE}=\widehat{HFE}$ (3) ($BCEF$ nội tiếp);

$\widehat{HFE}=\widehat{FHI}$ (4) (tam giác $FHI$ cân tại $I$).

Từ (1), (2), (3) và (4) suy ra $\widehat{BHK}=\widehat{FHI}$. Do $\Delta ABC$ nhọn nên hai điểm $I$ và $K$ nằm cùng phía với đường thẳng $HF$ nên ba điểm $H,I,K$ thẳng hàng.

 

Answer 13

  

Answer 14

1