Xét
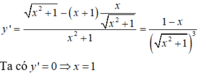
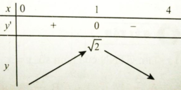
Ta có y' = 0 => x = 1
Vậy hàm số có GTLN bằng √2 khi x = 1 . Chọn đáp án A.
Xét
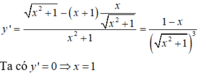

Ta có y' = 0 => x = 1
Vậy hàm số có GTLN bằng √2 khi x = 1 . Chọn đáp án A.
Cho hàm số y = x 2 - 2 | x | + 2 và các mệnh đề
(1) Hàm số trên liên tục trên R
(2) Hàm số trên có đạo hàm tại x = 0
(3) Hàm số trên đạt GTNN tại x = 0.
(4) Hàm số trên đạt GTLN tại x = 0.
(5) Hàm số trên là hàm chẵn
(6) Hàm số trên cắt trục hoành tại duy nhất một điểm
Trong các mệnh đề trên, số mệnh đề đúng là
A. 1
B. 2
C. 3
D. 4
Cho hàm số f(x) = x - 1 2 a x 2 + 4 a x - a + b - 2 , với a,b ∈ ℝ . Biết trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1. Hỏi trên đoạn - 2 ; - 5 4 , hàm số đạt giá trị nhỏ nhất tại giá trị nào của x?
A. x = - 5 4
B. x = - 4 3
C. x = - 3 2
D. x = -2
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Giá trị nhỏ nhất của hàm số f(x) = x +1/x trên nửa khoảng [2;+••] A:2 B:5/2 C:0 D:7/2
Có bao nhiêu mệnh đề đúng trong các phát biểu sau?
1. Hàm số không có đạo hàm tại x = 0.
2. Hàm số không liên tục tại x = 0.
3. Hàm số không có cực trị tại x = 0.
4. Hàm số đạt cực trị tại x = 0.
A. 0
B. 1
C. 2
D. 3
Giá trị thực của m để hàm số y = x - m 2 x + 1 đạt GTLN bằng 3 trên [-4;-2] là
A. m = ± 1
B. m = ± 5
C. m = 5
D. m = 1
a,Hàm số y = -2x + 1 không có cực trị.
Hàm số y = x/3 (x-3)2 đạt cực đại tại x = 1 và đạt cực tiểu tại x = 3.
chỉ mik cách lập nhóm nha
Trích một số bài toán trong đề:
+ Trên mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa mãn điều kiện /z/ = 2 là:
A. Đường tròn tâm O, bán kính R = 2
B. Đường tròn tâm O, bán kính R = 4
C. Đường tròn tâm O, bán kính R = 1/2
D. Đường tròn tâm O , bán kính R = căn 2
+ Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số y = f(x) có giá trị cực đại bằng 0
B. Giá trị lớn nhất của hàm số y = f(x) trên tập R là 1
C. Hàm số y = f(x) đạt cực đại tại x = 0 và cực tiểu tại x = -1
D. Hàm số y = f(x) có đúng một cực trị
+ Tìm phần thực của số phức (2 + 3i).i^10
Giá trị lớn nhất của hàm số sau trên khoảng (- ∞ ; + ∞ ) là:
y = 1 x 2 + x + 1
A. 1 B. 4/3
C. 5/3 D. 0