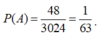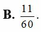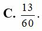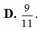Question

Gọi S là tập hợp các số tự nhiên gồm bốn chữ số đôi một khác nhau được lấy từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên một số từ S. Tính xác suất P để được một số chia hết cho 11 và tổng bốn chữ số của nó cũng chia hết cho 11.

A .   P   =   1 126

B .   P   =   2 63

C .   P   =   1 63

D .   P   =   3 126

Answer 1

Chọn C

Ta có 

Gọi số tự nhiên cần tìm có bốn chữ số là  a b c d ¯

Vì  a b c d ¯  chia hết cho 11 nên (a + c) - (b + d)  ⋮ 11

=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do 

Theo đề bài ta cũng có a + b + c + d chia hết cho 11

Mà 

hoặc 

Vì  nên  (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ 

(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số: 

- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2  cách.

- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn  d.

Vậy xác suất cần tìm là