Chọn A.
Phương trình hoành độ giao điểm:
x + 1 = 2 x + 4 x - 1 ⇔ x 2 - 2 x - 5 = 0
⇔ x = 1 + 6 x = 1 - 6
Suy ra hoành độ trung điểm của đoạn MN là
x 1 = 1 + 6 + 1 - 6 2 = 1
Chọn A.
Phương trình hoành độ giao điểm:
x + 1 = 2 x + 4 x - 1 ⇔ x 2 - 2 x - 5 = 0
⇔ x = 1 + 6 x = 1 - 6
Suy ra hoành độ trung điểm của đoạn MN là
x 1 = 1 + 6 + 1 - 6 2 = 1
Trong mặt phẳng Oxy , cho hình bình hành ABCD với A(3;2) ; D(4;1). Biết điểm B di động trên đường tròn (C):(x-2)^2+(y+1)^2=32 điểm C thuộc đường thẳng (d):x+y-1=0 .Biết rằng C có hoành độ dương . Tọa độ điểm C là
1. Cho hình bình hành ABCD có tâm O, Gọi M, N lần lượt là trung điểm của AB, AO.
a) XĐ ảnh của tam giác AND qua phép tịnh tiến \(\overrightarrow{OC}\)
b)XĐ ảnh của tam giác AMN qua phép vị tự tâm O, tỉ số -2
2. trong mặt phẳng Oxy cho điểm M(1;-5),\(\overrightarrow{v}=\left(-2,1\right)\)đường thẳng d: x-4y+3=0,
đường tròn \(\left(C\right):\left(x+2\right)^2+\left(y-1\right)^2=5\)
a) tìm tọa độ M' là ảnh của M qua phép tịnh tiến vecto \(\overrightarrow{v}\)
b)Viết phương trình d' là ảnh của d qua phép quay tâm O, góc quay \(^{-90^o}\)
c) tìm phương trình (C') là ảnh của (C) qua phép vị tự tâm O, tỉ số 2.
3.
Cho đường thẳng (d): x-5y-4=0. Viết phương trình đường thẳng (d') ảnh của (d) qua phép vị tự tâm O , góc 90o và phép vị tự tâm I(-2,3) tỉ số -3
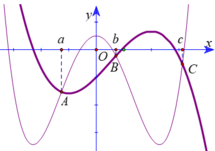
Cho hàm số y=f(x) và y=g(x) là hai hàm liên tục trên ℝ có đồ thị hàm số y = f '(x) là đường cong nét đậm và y = g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của y=f '(x) và y=g'(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) = f(x) - g(x) trên đoạn [a;c]?
![]()
![]()
![]()
![]()
Cho hàm số $y=f\left( x \right)={{x}^{3}}-3{{x}^{2}}+x-1$ có đồ thị là đường cong $\left( C \right)$. Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng $1$.
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình 3x – y + 9 = 0 và đường tròn (C) có phương trình: x 2 + y 2 + 2 x − 6 y + 6 = 0 .
Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đường tròn (C’) theo thứ tự là ảnh của M, d và (C) qua
a) Phép đối xứng qua gốc tọa độ;
b) Phép đối xứng qua tâm I.
Tìm m để đường thẳng d : y = - 1 cắt đồ thị (C) của hàm số y = x 4 - ( 3 m + 2 ) x 2 + 3 m tại bốn điểm phân biệt có hoành độ nhỏ hơn 2
![]()
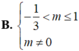
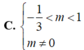
![]()
Trong mặt phẳng toạ độ, cho đồ thị (d) của hàm số y= 4x-5.
Với mỗi số nguyên dương, gọi An là giao điểm của(d) và đường thẳng x=n. Xét dãy số (un) với un là tung độ của điểm An. Tính u 1 + . . . + u 15 .
A. 405
B. 305
C. 205
D. 105
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
Trong mặt phẳng tọa độ Oxy cho điểm A(9,0) và đường tròn (C): x - 2 2 + y - 1 2 = 25 . Gọi ∆1;∆2 là hai tiếp tuyến của (C) đi qua A. Tính tổng khoảng cách từ O đến hai đường thẳng ∆1;∆2.
A. 36 5
B. 37 5
C. 73 5
D. 63 5