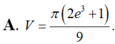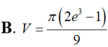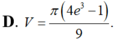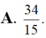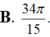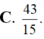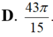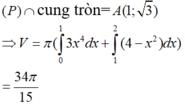Các câu hỏi tương tự
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số
y
x
, cung tròn có phương trình
y
6
-
x
2
(
-
6
≤
x
≤
6
)
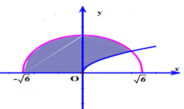
và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
Đọc tiếp
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình y = 6 - x 2 ( - 6 ≤ x ≤ 6 ) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
![]()
![]()
Thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường
y
tan
x
,
x
0
,
x
π
3
và trục hoành bằng
Đọc tiếp
Thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = tan x , x = 0 , x = π 3 và trục hoành bằng
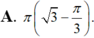
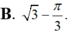
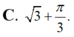
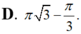
Gọi (H) là hình phẳng giới hạn bởi các đồ thì hàm số y tan x, trục hoành và các đường thẳng x 0,
x
π
4
. Quay (H) xung quanh trục Ox ta được khối tròn xoay có thể tích bằng
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi các đồ thì hàm số y = tan x, trục hoành và các đường thẳng x = 0, x = π 4 . Quay (H) xung quanh trục Ox ta được khối tròn xoay có thể tích bằng
![]()
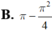
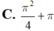
![]()
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
(
x
-
2
)
.
e
2
x
, trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng
π
(
e
a
+
b...
Đọc tiếp
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = ( x - 2 ) . e 2 x , trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng π ( e a + b ) c . Khi đó a+b+c bằng
A. 2
B. 56
C. -1
D. -24
Tính thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường ytanx; x0;
x
π
3
và trục hoành.
Đọc tiếp
Tính thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y=tanx; x=0; x = π 3 và trục hoành.
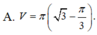
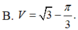

![]()
Cho (H) là hình phẳng giới hạn bởi parabol
y
x
2
và đường tròn
x
2
+
y
2
2
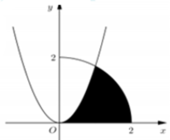
(phần tô đậm trong hình). Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục hoành.
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi parabol y = x 2 và đường tròn x 2 + y 2 = 2 (phần tô đậm trong hình). Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục hoành.
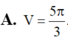
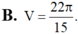
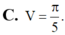
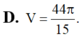
Cho (H) là hình phẳng giới hạn bởi
1
4
cung tròn có bán kính R2, đường cong
y
4
-
x
và trục hoành ( miền tô đậm như hình vẽ). Tính thể tích V của khối tạo thành khi cho hình (H) quay quanh trục Ox.
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi 1 4 cung tròn có bán kính R=2, đường cong y = 4 - x và trục hoành ( miền tô đậm như hình vẽ). Tính thể tích V của khối tạo thành khi cho hình (H) quay quanh trục Ox.
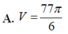
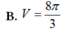
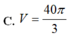
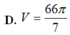
Thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường
y
x
ln
x
, xe và trục hoành là.
Đọc tiếp
Thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = x ln x , x=e và trục hoành là.
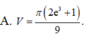
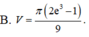
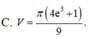
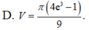
Thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường
y
x
ln
x
,
x
e
và trục hoành là
Đọc tiếp
Thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = x ln x , x = e và trục hoành là