Question

Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng: Các đường trung tuyến của tam giá BGD bằng một nửa các cạnh của tam giác ABC.

Answer 1

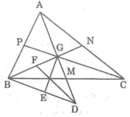
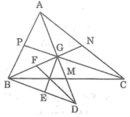
Ta có: GM = MD (chứng minh trên)

Suy ra BM là đường trung tuyến của tam giác BGD.

Suy ra: BM = 1/2 BC (4)

Kẻ đường trung tuyến GE và DF của tam giác BGD, ta có:

FG = 1/2 BG (tính chất đường trung tuyến)

GN = 1/2 GB (tính chất đường trung tuyến)

Suy ra: FG = GN

Xét ΔDFG và ΔANG, ta có:

AG = GD (gt)

∠(DGF) = ∠(AGN) (đối đỉnh)

GF = GN (chứng minh trên)

Suy ra: ΔDFG = ΔANG (c.g.c) ⇒ DF = AN

Mà AN = 1/2 AC (gt)

Suy ra: DF = 1/2 AC (5)

Mặt khác: BD = CG (chứng minh trên)

ED = 1/2 BD (vì E là trung điểm BD)

GP = 1/2 CG (tính chất đường trung tuyến)

Suy ra: ED = GP

Lại có: ΔBMD = ΔCMG (chứng minh trên)

⇒ ∠(BDM) = ∠(CGM) hay ∠(EDG) = ∠(CGM)

(CGM) = (PGA) (đối đỉnh)

Suy ra: ∠(EDG) = ∠(PGA)

AG = GD (gt)

Suy ra: ΔPGA = ΔEDG (c.g.c) ⇒ GE = AP mà AP = 1/2 AB (gt)

Do đó: GE = 1/2 AB (6)

Từ (4), (5) và (6) suy ra các đường trung tuyến của ΔBGD bằng một nửa cạnh của ΔABC.