Question

Giúp tớ câu này với ạ

Answer 1

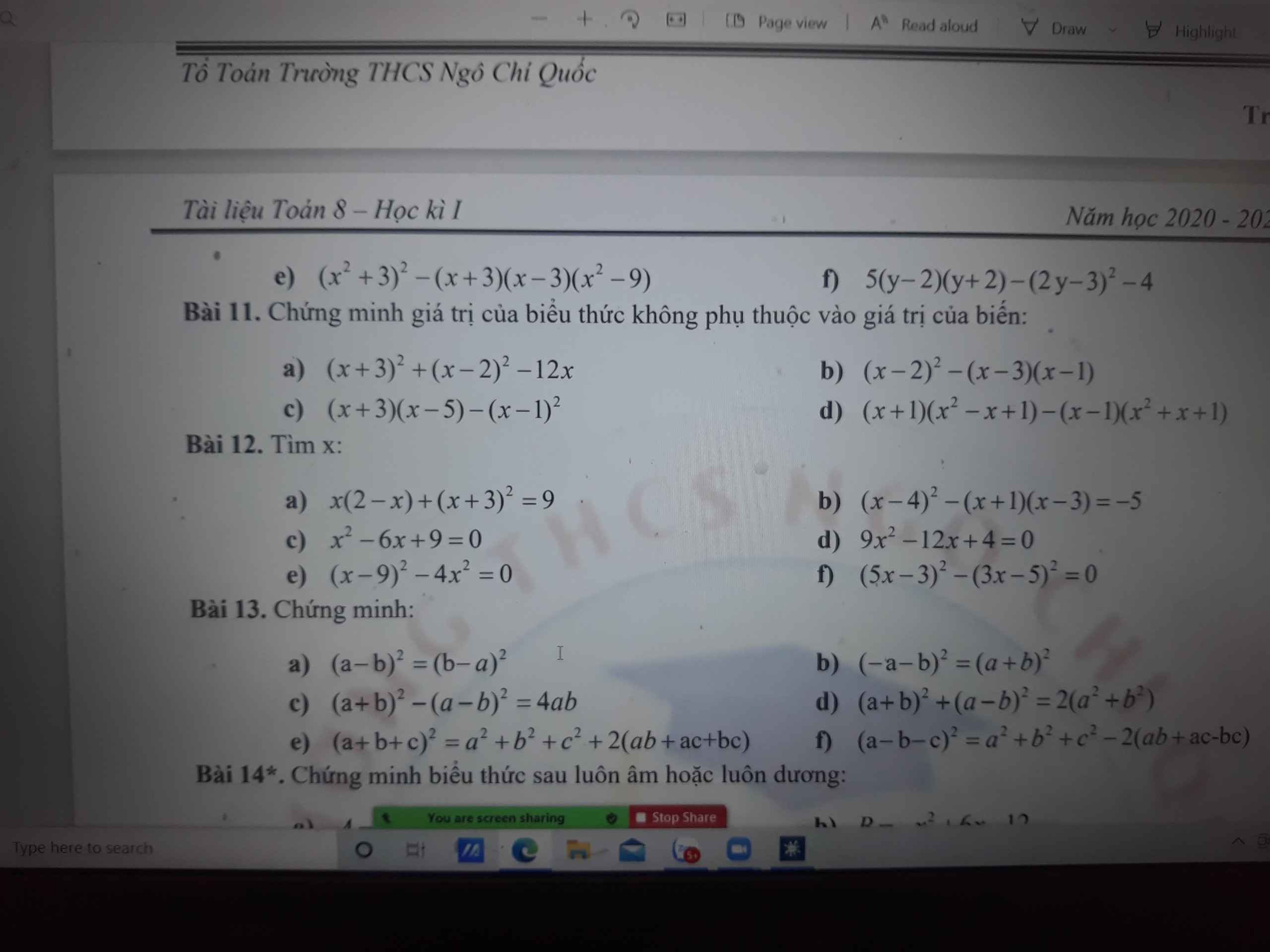
`a)A=x^2+4x+6=x^2+4x+4+2=(x+2)^2+2`

Vì `(x+2)^2 >= 0 AA x<=>(x+2)^2+2 >= 2 AA x`

  Hay `A >= 2 AA x`

Dấu "`=`" xảy ra `<=>(x+2)^2=0<=>x=-2`

____________________________________

`b)B=x^2-6x+10=x^2-6x+9+1=(x-3)^2+1`

Vì `(x-3)^2 >= 0 AA x<=>(x-3)^2+1 >= 1 AA x`

  Hay `B >= 1 AA x`

Dấu "`=`" xảy ra `<=>(x-3)^2=0<=>x=3`

____________________________________

`c)C=x^2+4x+y^2-2y-2010=x^2+4x+4+y^2-2y+1-2015=(x+2)^2+(y-1)^2-2015`

Vì `(x+2)^2 >= 0 AA x`  mà `(y-1)^2 >= 0 AA y`

 `=>(x+2)^2+(y-1)^2 >= 0 AA x,y`

`<=>(x+2)^2+(y-1)^2-2015 >= -2015 AA x,y`

  Hay `C >= -2015 AA x,y` 

Dấu "`=`" xảy ra `<=>{((x+2)^2=0<=>x=-2),((y-1)^2=0<=>y=1):}`

Answer 2

`a, A = x^2 + 4x + 4 + 2 = (x+2)^2 + 2 >= 0 + 2 = 2`

`b, x^2 - 6x + 10 = x^2 - 6x + 9 + 1 = (x-3)^2 + 1 >= 0 + 1= 1`

Answer 3

a, \(A=x^2+4x+6=x^2+2.x.2+2^2+2=\left(x+2\right)^2+2\ge2\forall x\in R\)

Dấu = xảy ra khi: \(\left(x+2\right)^2=0\Leftrightarrow x=-2\)

Vậy GTNN của A = 2 khi x = -2.

b, \(B=x^2-6x+10=x^2-2.x.3+3^2+1=\left(x-3\right)^2+1\ge1\forall x\in R\)

Dấu = xảy ra khi: \(\left(x-3\right)^2=0\Leftrightarrow x=3\)

Vậy GTNN của B = 1 khi x = 3.

c, \(C=x^2+4x+y^2-2y-2010\)

\(=\left(x^2+2.x.2+2^2\right)+\left(y^2-2.y.1+1\right)-2015\)

\(=\left(x+2\right)^2+\left(y-1\right)^2-2015\ge-2015\forall x,y\in R\)

Dấu = xảy ra khi: \(\left\{{}\begin{matrix}\left(x+2\right)^2=0\\\left(y-1\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=1\end{matrix}\right.\)

Vậy GTNN của C = -2015 khi x = -2, y = 1.

Answer 4

a, A=x^2+4x+6

A= x^2 + 4x+4+2

A=(x+2)^2 +2

(x+2)^2 lớn hơn hoặc = 0

=> (x+2)^2+2 lớn hơn hoặc =2

 dấu = xảy ra khi x+2=0=> x=-2

vậy bthức A đạt GTNN= 2 khi x=-2