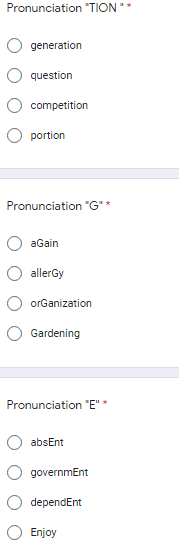
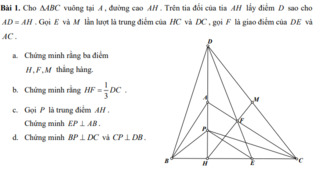
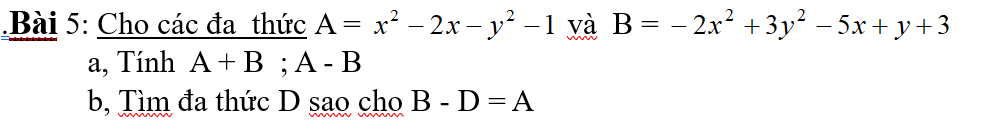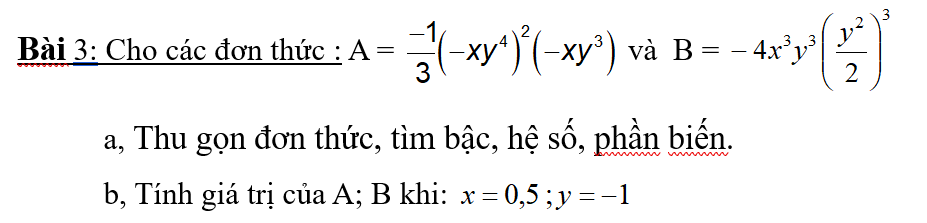a. Xét tam giác APM và tam giác ACN:
AP = AC (gt).
AM = AN (gt).
\(\widehat{A}\) chung.
=> Tam giác APM = Tam giác ACN (c - g - c).
b. Ta có: \(\widehat{PND}=180^o-\widehat{ANC};\widehat{CMD}=180^o-\widehat{AMP}.\)
Mà \(\widehat{ANC}=\widehat{AMP}\) (Tam giác APM = Tam giác ACN).
=> \(\widehat{PND}=\widehat{CMD.}\)
Ta có: NP = AP - AN; MC = AC - AM.
Mà AN = AM; AP = AC (gt).
=> NP = MC.
Xét tam giác NDP và tam giác MDC:
NP = MC (cmt).
\(\widehat{NPD}=\widehat{MCD}\) (Tam giác APM = Tam giác ACN).
\(\widehat{PND}=\widehat{CMD}\) (cmt).
=> Tam giác NDP = Tam giác MDC (g - c - g).
Ta có: MC = AC - AM; NB = AB - AN.
Mà AM = AN; AC < AB (gt).
=> MC < NB.
=> \(\widehat{BMN}=\widehat{CNM}.\) => \(\widehat{OMN}=\widehat{ONM}.\)