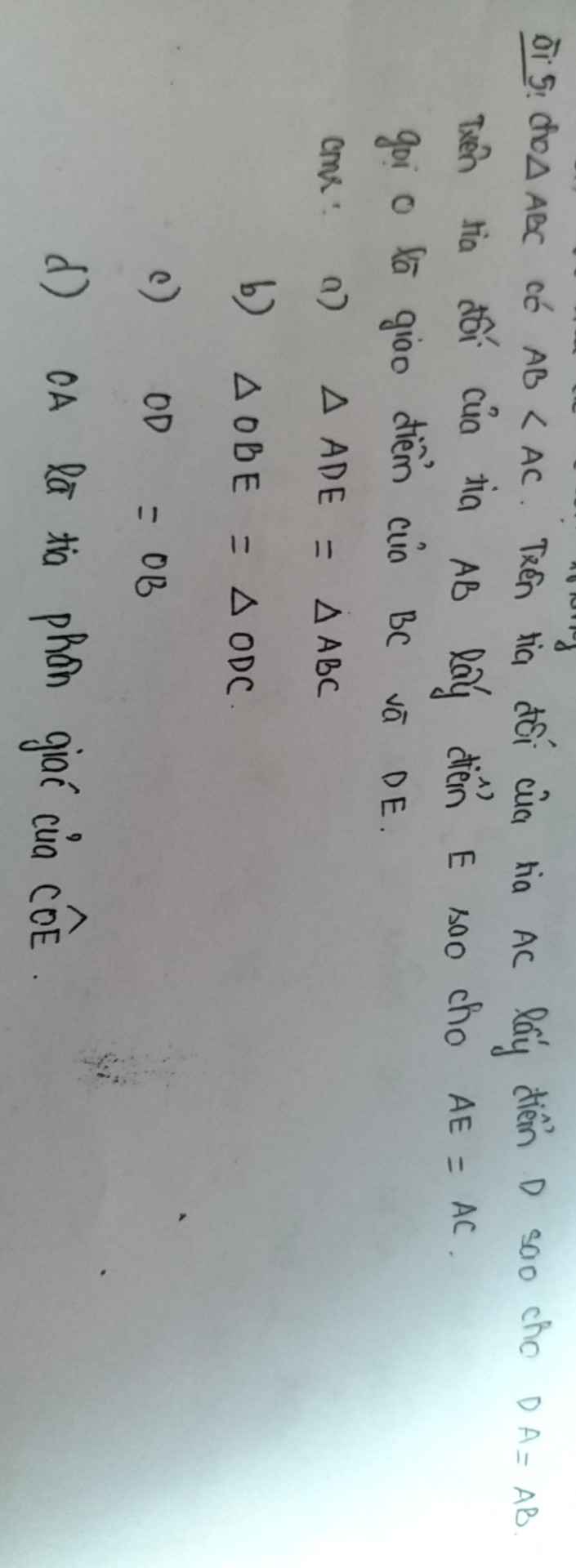a) Xét \(\Delta ADE\) và \(\Delta ABC:\)
\(AD=AB\left(gt\right).\\ AE=AC\left(gt\right).\)
\(\widehat{DAE}=\widehat{BAC}\) (2 góc đối đỉnh).
\(\Rightarrow\Delta ADE=\Delta ABC\left(c-g-c\right).\)
b) Ta có: \(\widehat{OBE}=180^o-\widehat{ABC};\widehat{ODC}=180^o-\widehat{ADE}.\)
Mà \(\widehat{ABC}=\widehat{ADE}\left(\Delta ABC=\Delta ADE\right).\)
\(\Rightarrow\widehat{OBE}=\widehat{ODC}.\)
Ta có: \(BE=BA+AE;DC=DA+AC.\)
Mà \(BA=DA;AE=AC\left(gt\right).\)
\(\Rightarrow BE=DC.\)
Xét \(\Delta OBE\) và \(\Delta ODC:\)
\(\widehat{OBE}=\widehat{ODC}\left(cmt\right).\\ BE=DC\left(cmt\right).\\ \widehat{BEO}=\widehat{DCO}\left(\Delta ADE=\Delta ABC\right).\\ \Rightarrow\Delta OBE=\Delta ODC\left(g-c-g\right).\)
c) \(\Delta OBE=\Delta ODC\left(cmt\right).\)
\(\Rightarrow OB=OD\) (2 cạnh tương ứng).
d) Xét \(\Delta OAE\) và \(\Delta OAC:\)
\(OAchung.\\ OE=OC\left(\Delta OBE=\Delta ODC\right).\\ AE=AC\left(gt\right).\\ \Rightarrow\Delta OAE=\Delta OAC\left(c-c-c\right).\)
\(\Rightarrow\widehat{AOE}=\widehat{AOC}\) (2 góc tương ứng).
\(\Rightarrow OA\) là tia phân giác của \(\widehat{COE}.\)