Bài tập 5:
a. \(A=\left(2x^2+4x+2\right)+13\)
\(=2\left(x^2+2x+1\right)+13\)
\(=2\left(x+1\right)^2+13\ge13\)
Dấu "=" xảy ra \(\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
Vậy \(MinA=13\Leftrightarrow x=-1\)
b. \(B=3x^4+x^2+10\ge10\)
Dấu "=" xảy ra \(\Leftrightarrow x=0\)
Vậy \(MinB=10\Leftrightarrow x=0\)
c. \(B=4x^2+3x+5\)
\(=\left(4x^2+2.\dfrac{3}{4}.2x+\dfrac{9}{16}\right)-\dfrac{9}{16}+5\)
\(=\left(2x+\dfrac{3}{4}\right)^2+\dfrac{71}{16}\ge\dfrac{71}{16}\)
Dấu "=" xảy ra \(\Leftrightarrow2x+\dfrac{3}{4}=0\Leftrightarrow x=-\dfrac{3}{8}\)
Vậy \(MinC=\dfrac{71}{16}\Leftrightarrow x=-\dfrac{3}{8}\)
d. \(D=\left(x+5\right)\left(x-1\right)\left(x^2+4x+5\right)\)
\(=\left(x^2+4x-5\right)\left(x^2+4x+5\right)\)
\(=\left[\left(x^2+4x\right)-5\right]\left[\left(x^2+4x\right)+5\right]\)
\(=\left(x^2+4x\right)^2-25\ge-25\)
Dấu "=" xảy ra \(\Leftrightarrow x^2+4x=0\Leftrightarrow x\left(x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
Vậy \(MinD=-25\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
Bài tập 6:
a. \(A=\left(x-1\right)^3-\left(x+1\right)^3-3\left(2x^2-1\right)\)
\(=\left(x^3-3x^2+3x-1\right)-\left(x^3+3x^2+3x+1\right)-\left(6x^2-3\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6x^2+3\)
\(=-12x^2+1\)
b. \(B=4\left(x-2\right)\left(x+2\right)-\left(x-1\right)\left(x^2+x+1\right)+x^2\left(x-2\right)-2\left(x^2+1\right)\)
\(=4\left(x^2-4\right)-\left(x^3-1\right)+\left(x^3-2x^2\right)-\left(2x^2+2\right)\)
\(=4x^2-16-x^3+1+x^3-2x^2-2x^2-2\)
\(=-17\)
c. \(C=\left(y-x+1\right)^2+2\left(x-y\right)\left(1+y-x\right)+\left(x-y\right)^2\)
\(=\left(y-x+1\right)^2+2\left(x-y\right)\left(y-x+1\right)+\left(x-y\right)^2\)
\(=\left[\left(y-x+1\right)+\left(x-y\right)\right]^2\)
\(=\left(y-x+1+x-y\right)^2\)
\(=1\)
giúp mình bài này với ạ,ghi từng bước giúp mình lun ạ
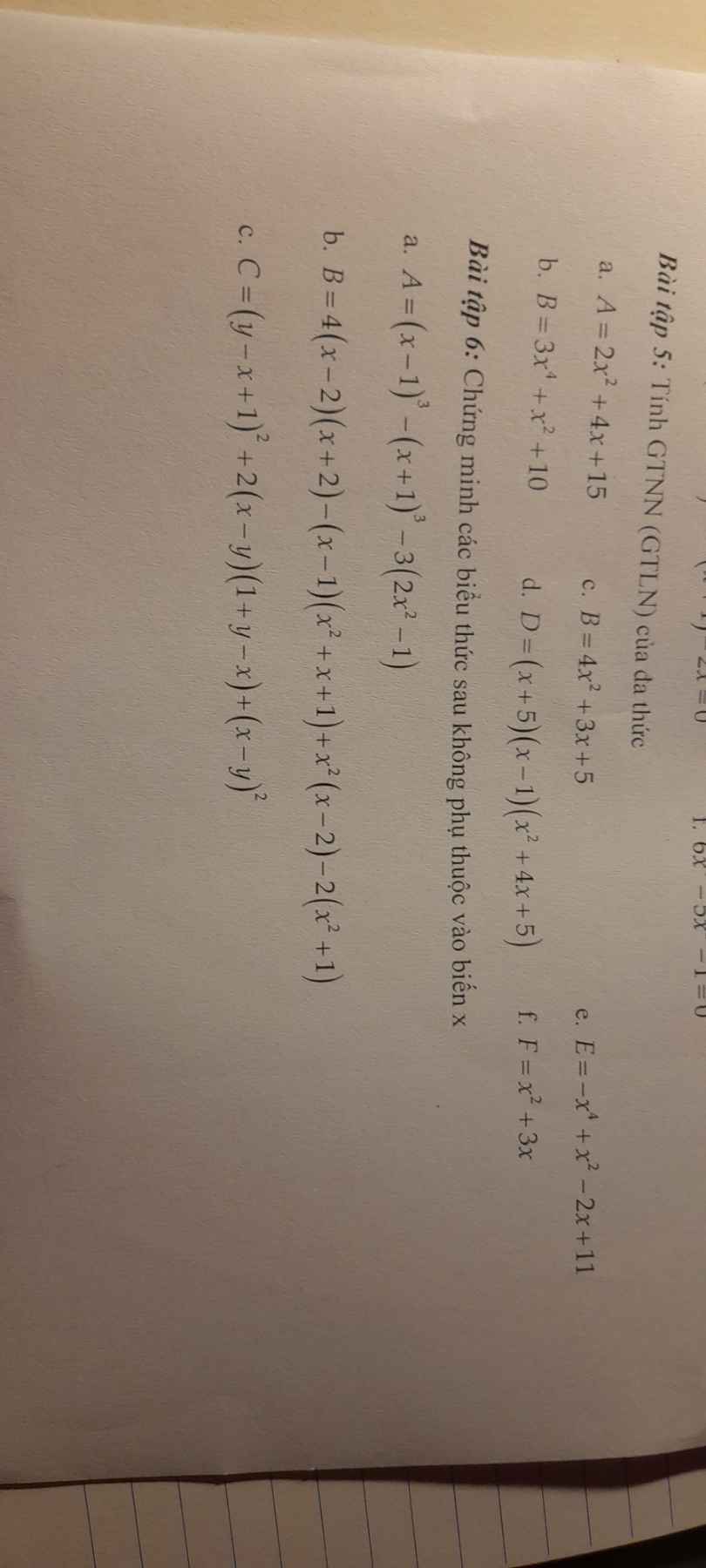
giúp mình với ạ, mình cần gấp lắm ạ
