a) \(a^2\left(a+1\right)+2a\left(a+1\right)\\ =\left(a^2+2a\right)\left(a+1\right)=a\left(a+1\right)\left(a+2\right)\)
Vì a,a+1,a+2 là 3 số nguyên liên tiếp nên có 1 số chia hết cho 2, 1 số chia hết cho 3
Mà (2,3)=1⇒a(a+1)(a+2)⋮(2.3)=6
Vậy \(a^2\left(a+1\right)+2a\left(a+1\right)⋮6\)
a) \(a^2\left(a+1\right)+2a\left(a+1\right)=\left(a+1\right)\left(a^2+2a\right)=a\left(a+1\right)\left(a+2\right)\) là tích 3 số nguyên liên tiếp nên có một số chia hết cho 2 và một số chia hết cho 3
\(\Rightarrow a^2\left(a+1\right)+2a\left(a+1\right)⋮2.3=6,\forall a\in Z\)
b) \(a\left(2a-3\right)-2a\left(a+1\right)=2a^2-3a-2a^2-2a=-5a⋮5,\forall a\in Z\)
c) \(\left(2a-1\right)^3-\left(2a-1\right)=\left(2a-1\right)\left[\left(2a-1\right)^2-1\right]=\left(2a-1\right)\left(2a-1-1\right)\left(2a-1+1\right)=\left(2a-2\right)\left(2a-1\right)2a=4\left(2a-1\right)\left(a-1\right)a\)
Do \(\left(a-1\right)a\) là tích 2 số nguyên liên tiếp nên chia hết cho 2 \(\Rightarrow4a\left(a-1\right)⋮8\Rightarrow4\left(2a-1\right)\left(a-1\right)a⋮8\Rightarrow\left(2a-1\right)^3-\left(2a-1\right)⋮8,\forall a\in Z\)
d) \(a^3-19a=a^3-a-18a=a\left(a^2-1\right)-18a=\left(a-1\right)a\left(a+1\right)-18a\)
Ta có \(\left(a-1\right)a\left(a+1\right)⋮6,-18a⋮6,\forall a\in Z\)
Nên suy ra \(a^3-19a⋮6,\forall a\in Z\)
a: Ta có: \(a^2\left(a+1\right)+2a\left(a+1\right)\)
\(=a\left(a+1\right)\left(a+2\right)\)
Vì a;a+1;a+2 là ba số tự nhiên liên tiếp nên \(a\left(a+1\right)\left(a+2\right)⋮3!=6\)
b: Ta có: \(a\left(2a-3\right)-2a\left(a+1\right)\)
\(=2a^2-3a-2a^2-2a\)
\(=-5a⋮5\)

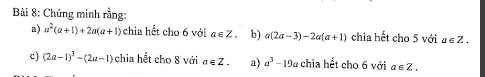

















 Giúp em câu này vs ạ
Giúp em câu này vs ạ
