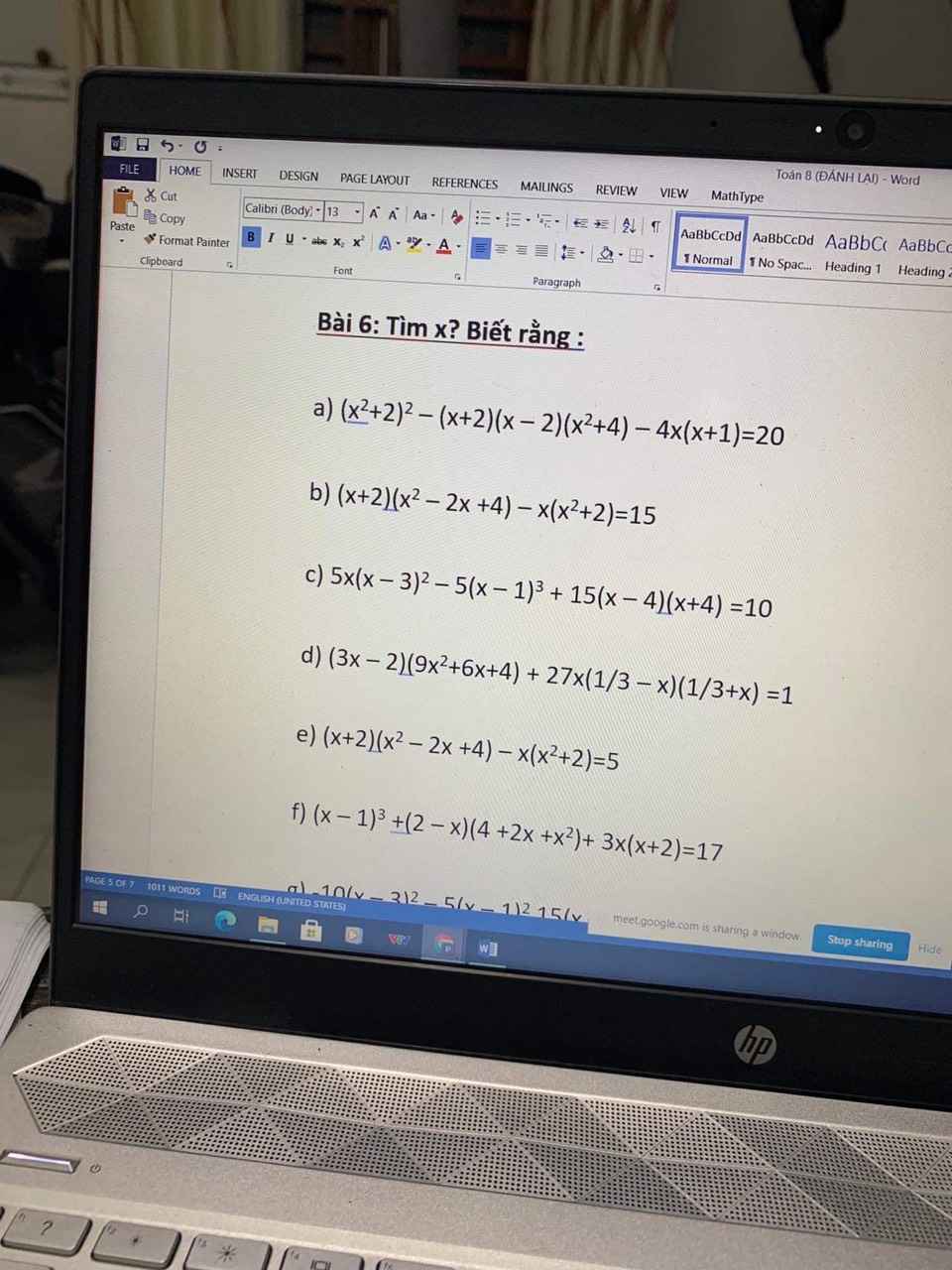
\(a.\left(x^2+2\right)^2-\left(x+2\right)\left(x-2\right)\left(x^2+4\right)-4x\left(x+1\right)=20\)
\(-4x+20=20\)
\(-4x=20-20\)
\(-4x=0\)
\(x=0:\left(-4\right)\)
\(x=0.\)
\(Vậy...\)
\(b.\left(x+2\right)\left(x^2-2x+4\right)-x\left(x^2+2\right)=15\)
\(x^3+8-x^3-2x=15\)
\(-2x+8=15\)
\(-2x=15-8\)
\(-2x=7\)
\(x=7:\left(-2\right)\)
\(x=-\dfrac{7}{2}.\)
\(Vậy...\)
\(c.5x\left(x-3\right)^2-5\left(x-1\right)^3+15\left(x-4\right)\left(x+4\right)=10\)
\(30x-235=10\)
\(30x=10+235\)
\(30x=245\)
\(x=245:30\)
\(x=\dfrac{49}{6}.\)
\(Vậy...\)
\(d.\left(3x-2\right)\left(9x^2+6x+4\right)+27x\left(\dfrac{1}{3}-x\right)\left(\dfrac{1}{3}+x\right)=1\)
\(3x-8=1\)
\(3x=1+8\)
\(3x=9\)
\(x=9:3\)
\(x=3\)
\(Vậy...\)
\(e.\left(x+2\right)\left(x^2-2x+4\right)-x\left(x^2+2\right)=5\)
\(-2x+8=5\)
\(-2x=5-8\)
\(-2x=-3\)
\(x=-3:\left(-2\right)\)
\(x=\dfrac{3}{2}.\)
\(Vậy...\)
\(f.\left(x-1\right)^3+\left(2-x\right)\left(4+2x+x^2\right)+3x\left(x+2\right)=17\)
\(9x+7=17\)
\(9x=17-7\)
\(9x=10\)
\(x=10:9\)
\(x=\dfrac{10}{9}\)
\(Vậy...\)