a) nhân dạng liên hiệp
<=> \(\dfrac{4\left(\sqrt{7}+3\right)}{2}-\dfrac{3\left(\sqrt{7}+2\right)}{3}\)
= 2\(\sqrt{7}+6-\sqrt{7}-2\) = \(\sqrt{7}+4\)
b) (\(\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}+1}-\sqrt{x}\)).\(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
<=> ( x - \(\sqrt{x}+1-\sqrt{x}\) ) . \(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
<=> \(\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)}\)= \(\dfrac{\sqrt{x}-1}{\sqrt{x}}\)

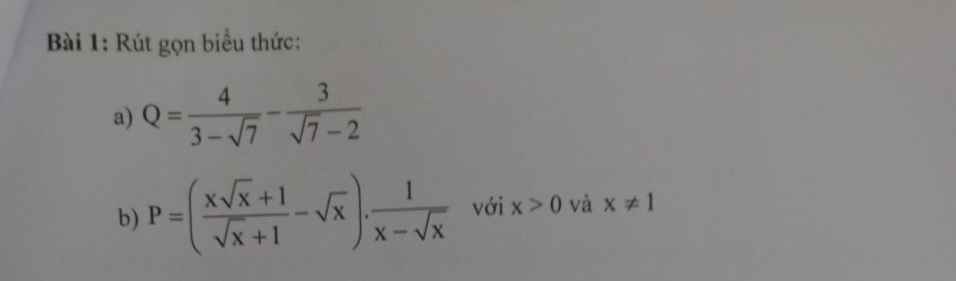









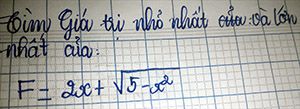

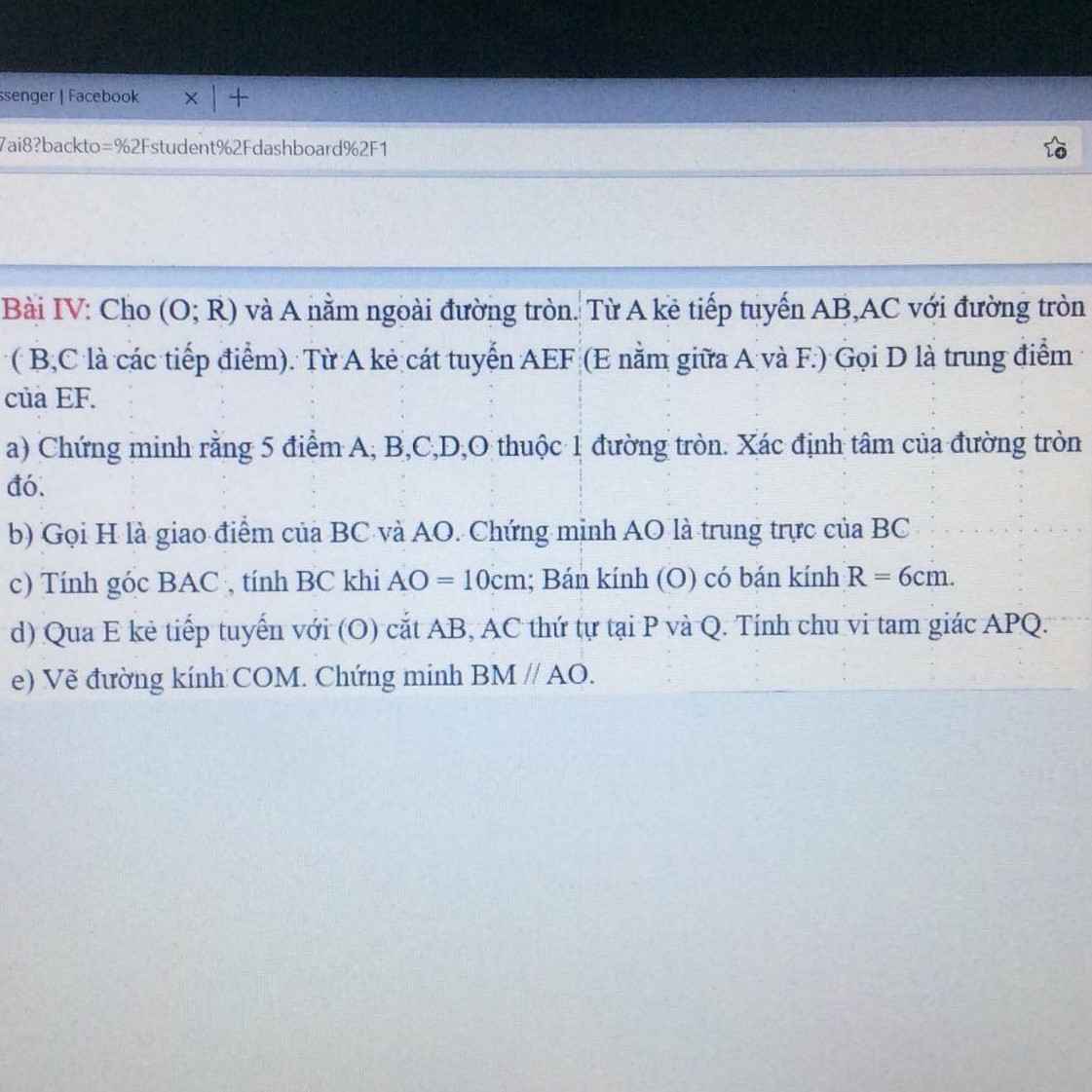

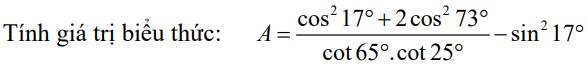



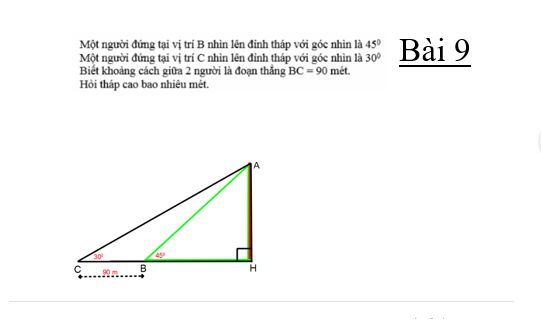 giúp em với ạ. Em cảm ơn ạ
giúp em với ạ. Em cảm ơn ạ