\(\dfrac{x-3}{3x-5}< \dfrac{3x-5}{x-3}.\left(x\ne3;x\ne\dfrac{5}{3}\right).\)
\(\Leftrightarrow\dfrac{x-3}{3x-5}-\dfrac{3x-5}{x-3}< 0.\Leftrightarrow\dfrac{\left(x-3\right)^2-\left(3x-5\right)^2}{\left(3x-5\right)\left(x-3\right)}< 0.\)
\(\Leftrightarrow\dfrac{x^2-6x+9-\left(9x^2-30x+25\right)}{\left(3x-5\right)\left(x-3\right)}< 0.\) \(\Leftrightarrow\dfrac{x^2-6x+9-9x^2+30x-25}{\left(3x-5\right)\left(x-3\right)}< 0.\)
\(\Leftrightarrow\dfrac{-8x^2+24x-16}{\left(3x-5\right)\left(x-3\right)}< 0.\Leftrightarrow\dfrac{8x^2-24x+16}{\left(3x-5\right)\left(x-3\right)}>0.\)
\(\Leftrightarrow\dfrac{8\left(x^2-3x+2\right)}{\left(3x-5\right)\left(x-3\right)}>0.\Leftrightarrow\dfrac{\left(x-2\right)\left(x-1\right)}{\left(3x-5\right)\left(x-3\right)}>0.\)
Đặt \(\dfrac{\left(x-2\right)\left(x-1\right)}{\left(3x-5\right)\left(x-3\right)}=f\left(x\right).\)
Lập bảng xét dấu:
| x | \(-\infty\) 1 \(\dfrac{5}{3}\) 2 3 \(+\infty\) |
| x - 2 | - | - | - 0 + | + |
| x - 1 | - 0 + | + | + | + |
| 3x - 5 | - | - 0 + | + | + |
| x - 3 | - | - | - | - 0 + |
| f (x) | + 0 - || + 0 - || + |
Vậy \(\dfrac{\left(x-2\right)\left(x-1\right)}{\left(3x-5\right)\left(x-3\right)}=f\left(x\right)>0.\) \(\Leftrightarrow x\in\left(-\infty;1\right)\cup\left(\dfrac{5}{3};2\right)\cup\left(3;+\infty\right).\)
a)
\(\left\{{}\begin{matrix}2x^2+7x-4\ge x^2-4\\\dfrac{2x-1}{x^2+x-2}< \dfrac{2x-5}{x^2+x-2}\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x^2+7\ge0\\\dfrac{2x-5-2x+1}{x^2+x-2}>0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x\left(x+7\right)\ge0\\\dfrac{-4}{x^2+x-2}>0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x\left(x+7\right)\ge0\\\left(x-1\right)\left(x+2\right)< 0\end{matrix}\right.\)
ta có x+2>x-1
=>x-1<0 và x+2 >0 để thỏa điều kiện =>x<1 và x>-2(hay -2<x<1)(1)
vì -2<x<1 nên x+7>0
=>x\(\ge\)0 để thỏa điều kiện(2)
từ (1) và (2) =>0\(\le\)x<1
b)
\(\left\{{}\begin{matrix}\left(x-3\right)\left(\sqrt{2}-x\right)>0\\4x-3< 2\left(x+3\right)\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}\left(x-3\right)\left(\sqrt{2}-x\right)>0\\2x-9< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}\left(x-3\right)\left(\sqrt{2}-x\right)>0\\x< \dfrac{9}{2}\end{matrix}\right.\)
có 2 TH xảy ra để thỏa điều kiện
TH1 (x-3)<0 và (\(\sqrt{2}\)-x)<0=>\(\sqrt{2}\)<x<3(nhận)
TH2 (x-3)>0 và (\(\sqrt{2}\)-x)>0=>3<x<\(\sqrt{2}\)(loại)
em nghĩ như nào làm như v thôi có gì sai chị xem và sửa hộ em nhá 
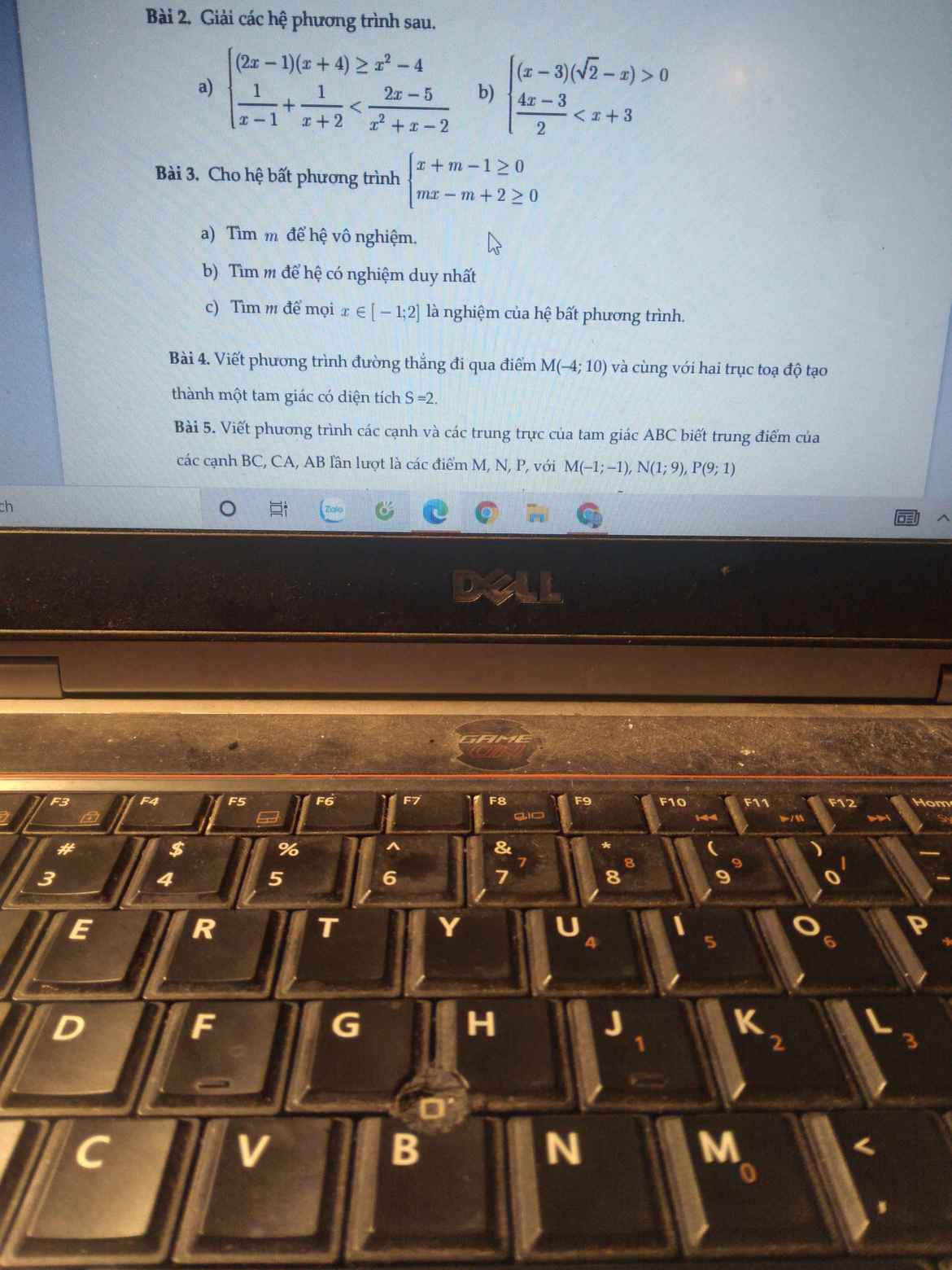
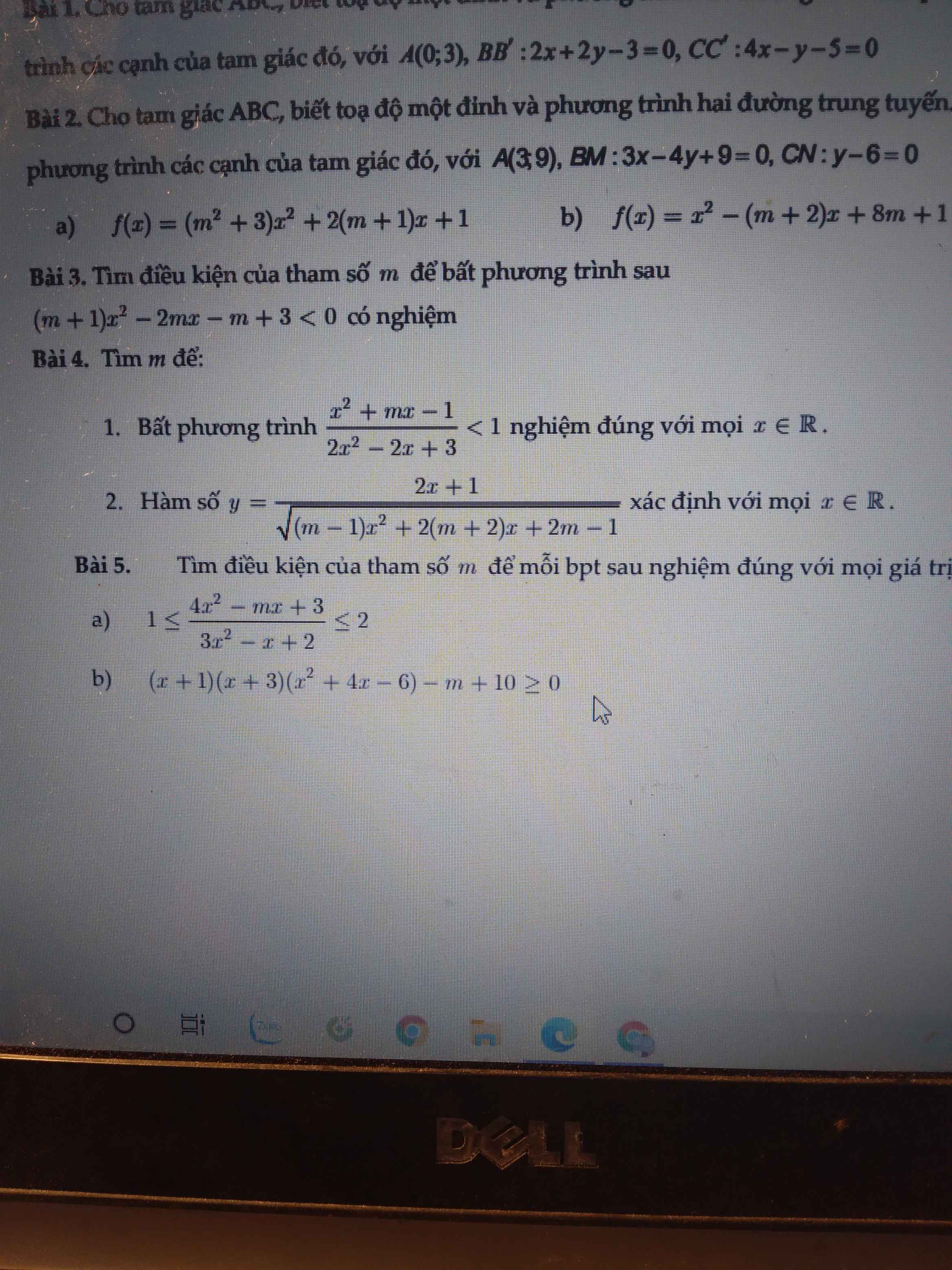
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
