1
a
\(=x\left(x^2+xy\right)-z\left(x^2+xy\right)\\ =\left(x-z\right)\left(x^2+xy\right)\)
b
\(=12\left(xy-xz\right)+3x\left(xy-xz\right)\\ =\left(12+3x\right)\left(xy-xz\right)\\ =x\left(12+3x\right)\left(y-z\right)\)
c
\(=\dfrac{1}{2}\left(x^4+2x^2y^2+y^4\right)-\dfrac{1}{2}.4x^2y^2\\ =\dfrac{1}{2}\left(x^4+2x^2y^2+y^4-4x^2y^2\right)\\ =\dfrac{1}{2}\left(x^4-2x^2y^2+y^4\right)\\ =\dfrac{1}{2}\left(x^2-y^2\right)^2\\ =\dfrac{1}{2}\left(x^2-y^2\right)\left(x^2-y^2\right)\\ =\dfrac{1}{2}\left(x-y\right)\left(x+y\right)\left(x-y\right)\left(x+y\right)\)
d
\(=2\left(x-y\right)^2-2.\left(5xy\right)^2\\ =2\left[\left(x-y\right)^2-\left(5xy\right)^2\right]\\ =2\left(x-y-5xy\right)\left(x-y+5xy\right)\)
2
\(5x^2z-10xyz+5y^2z\\ =5x^2z-5xyz-5xyz+5y^2z\\ =\left(5x^2z-5xyz\right)-\left(5xyz-5y^2z\right)\\ =5xz\left(x-y\right)-5yz\left(x-y\right)\\ =\left(5xz-5yz\right)\left(x-y\right)\\ =5z\left(x-y\right)\left(x-y\right)\\=5z\left(x-y\right)^2\)
Thế \(x=124;y=24;z=2\) vào biểu thức được:
\(5.2\left(124-24\right)^2=10.\left(100\right)^2=10.10000=100000\)









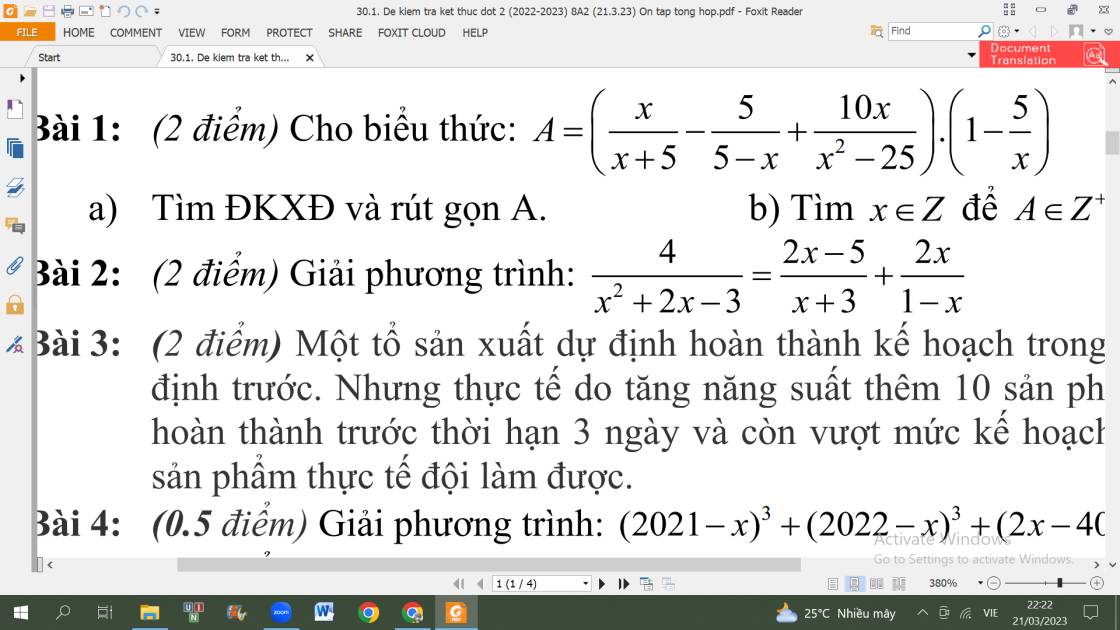



 Giải bài 4 và bài 5 và bài 6 nhớ giải chi tiết giúp mik
Giải bài 4 và bài 5 và bài 6 nhớ giải chi tiết giúp mik




