x2 = 12x + 288
⇔ x2 – 12x – 288 = 0
Có a = 1; b’ = -6; c = -288; Δ’ = b’2 – ac = (-6)2 – 1.(-288) = 324 > 0
Phương trình có hai nghiệm:
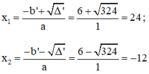
Vậy phương trình có hai nghiệm x1 = 24 và x2 = -12.
x2 = 12x + 288
⇔ x2 – 12x – 288 = 0
Có a = 1; b’ = -6; c = -288; Δ’ = b’2 – ac = (-6)2 – 1.(-288) = 324 > 0
Phương trình có hai nghiệm:
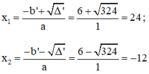
Vậy phương trình có hai nghiệm x1 = 24 và x2 = -12.
Giải vài phương trình của An Khô-va-ri-zmi (xem Toán 7, Tập 2, tr.26): 1 12 x 2 + 7 12 x = 19
Giải vài phương trình của An Khô-va-ri-zmi (xem Toán 7, Tập 2, tr.26):
a ) x 2 = 12 x + 288 b ) 1 12 x 2 + 7 12 x = 19
Giải bất phương trình sau: \(\dfrac{x^2-26}{10}\)+\(\dfrac{x^2-25}{11}\) \(\ge\) \(\dfrac{x^2-24}{12}\)+\(\dfrac{x^2-23}{13}\)
giải phương trình: \(\left(2x^2-10x+12\right)\sqrt{\frac{x+2}{x-2}}=-x^3+3x^2+12x-26\)
một vài bài sử dụng \(\Delta^'\)(cơ bản )
bài 1 : Không giải phương trình, hãy xác định xem phương trình có bao nhiêu nghiệm?
\(x^2+7x+18=0\)
bài 2: Tìm giá trị của tham số m để phương trình \(x^2+2mx-m+4=0\)có nghiệm ( hơi hơi nâng cao)
7. Phương trình bậc hai.
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠0)

\(2x-x^2-\sqrt{6x^2-12+7}=0\)
Giải phương trình
Giải hệ phương trình : \(\left\{{}\begin{matrix}x^3-2y^2-12y=26\\x^2y^2+9x^2-3y^2-6y=27\end{matrix}\right.\)
Giải phương trình : \(\left(\dfrac{x}{x+2}\right)^2=3x^2-6x-3\)
\(\sqrt{x+5}=x^2-5\)
\(\sqrt{x-1}-\sqrt[3]{2-x}=5\)
Giải phương trình trên tập N:
a, 3^x+7=y^3
b, 2^x+2^y=2^(x+y)