Điều kiện xác định: x ≠ ±2.
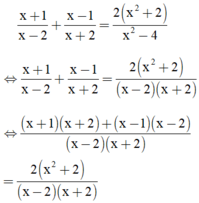
⇒ (x + 1)(x + 2) + (x – 1)(x – 2) = 2(x2 + 2)
⇔ x2 + x + 2x + 2 + x2 – x – 2x + 2 = 2x2 + 4
⇔ 2x2 + 4 = 2x2 + 4
⇔ 0x = 0.
Vậy phương trình nghiệm đúng với mọi x ≠ ±2.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Điều kiện xác định: x ≠ ±2.
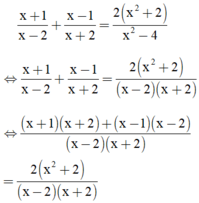
⇒ (x + 1)(x + 2) + (x – 1)(x – 2) = 2(x2 + 2)
⇔ x2 + x + 2x + 2 + x2 – x – 2x + 2 = 2x2 + 4
⇔ 2x2 + 4 = 2x2 + 4
⇔ 0x = 0.
Vậy phương trình nghiệm đúng với mọi x ≠ ±2.
giải phương trình |x+1|+|x-1|=1+|x^2-1|giải phương trình |x+1|+|x-1|=1+|x^2-1|giải phương trình |x+1|+|x-1|=1+|x^2-1|giải phương trình |x+1|+|x-1|=1+|x^2-1|giải phương trình |x+1|+|x-1|=1+|x^2-1|
giải phương trình 8(x+1/x)^2+4(x^2+1/x)^2-4(x^2+1/x^2)(x+1/x)^2=(x+4)^2
giải phương trình 8(x+1/x)^2+4(x^2+1/x^2)^2-4(x^2+1/x^2)(x+1/x)^2=(x+4)^2
Giải phương trình: 8(x+1/x)^2 + 4(x^2+1/x^2)^2 - 4(x^2+1/x^2)(x+1/x)^2=(x+4)^2
giải phương trình và bất phương trình
/x-5/=2x
(x-2)^2+2(x-1)<=x^2+4
giải phương trình:8(x+1/x)^2+4(x^2+1/x^2)^2=(x+4)^2
8(x+1/x)^2+4(x^2+1/x^2)^2-4(x^2+1/x^2)(x+1/x)^2=(x+4)^2
Giải phương trình
1.Giải phương trình
1.giải phương trình
\(\frac{x^4}{x^2-4x+4}+\frac{^{x^2}}{x-2}-2=0\)
e,x-2/2+x-3/x-2=2(x-11)/x^2-4
f,x+1/x-1-x-1/x+1=4/x^2-1