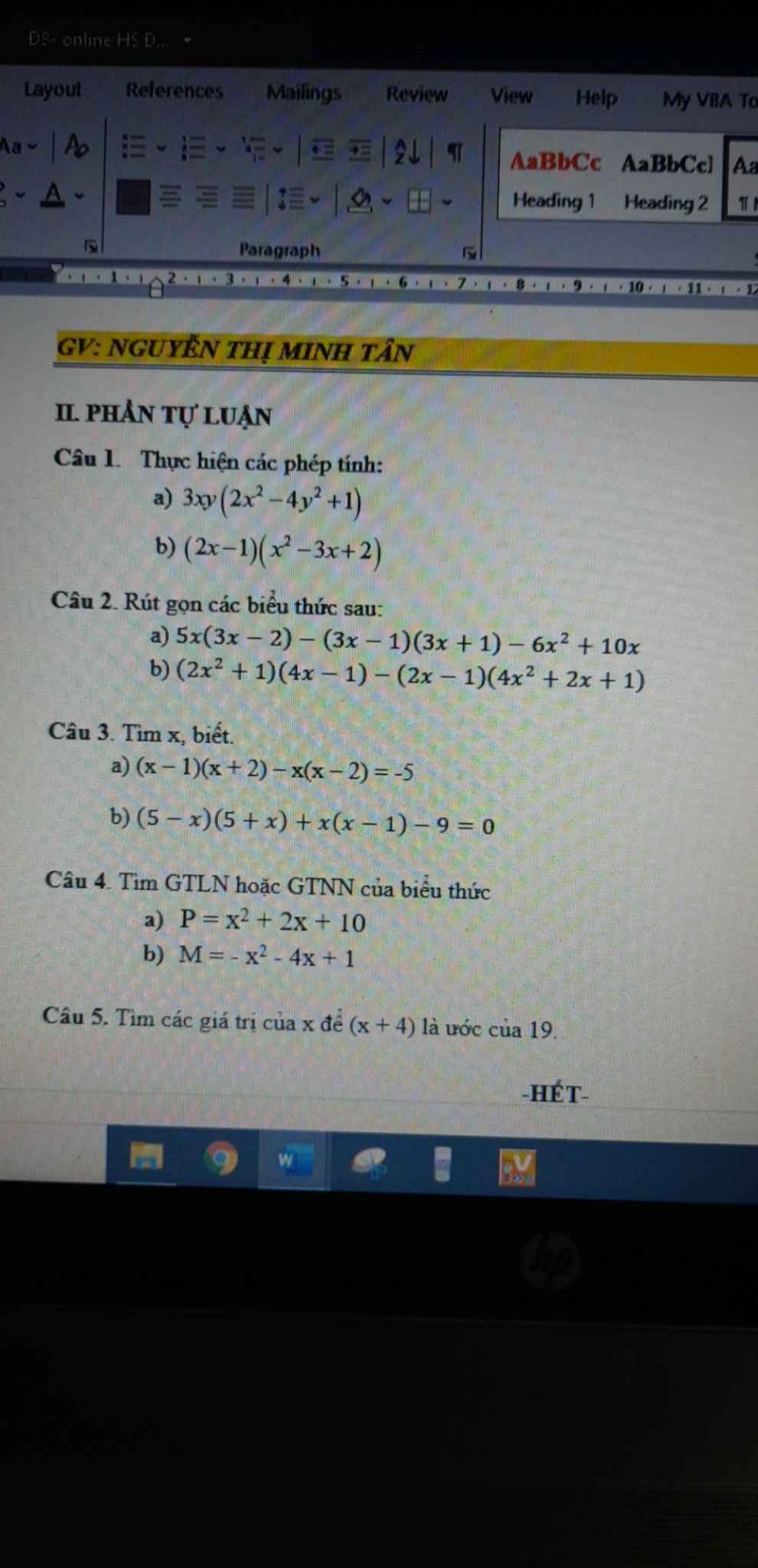
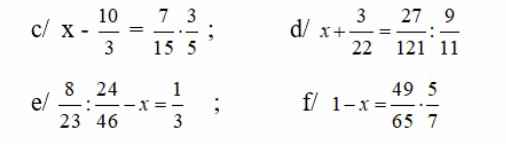câu 5đâu có thấy đâu
\(P=\frac{a}{a+1}+\frac{b}{b+1}+\frac{c}{c+1}\left(a,b,c>0\right)\)
Dễ dàng chứng minh được:
\(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\left(x,y>0\right)\left(1\right)\)(bạn hãy tự chứng minh).
Dấu bằng xảy ra \(\Leftrightarrow x=y>0\)
Ta có:
\(\frac{a}{a+1}=\frac{a}{a+a+b+c}\)(vì \(a+b+c=1\)).
\(\Rightarrow\frac{a}{a+1}=\frac{a}{\left(a+b\right)+\left(a+c\right)}\)
Vì \(a,b,c>0\)nên áp dụng bất đẳng thức (1), ta được
\(\frac{1}{a+b}+\frac{1}{a+c}\ge\frac{4}{\left(a+b\right)+\left(a+c\right)}\)
\(\Leftrightarrow\frac{1}{4}\left(\frac{1}{a+b}+\frac{1}{a+c}\right)\ge\frac{1}{\left(a+b\right)+\left(a+c\right)}\)
\(\Leftrightarrow\frac{1}{4}\left(\frac{a}{a+b}+\frac{a}{a+c}\right)\ge\frac{a}{\left(a+b\right)+\left(a+c\right)}\)
\(\Leftrightarrow\frac{1}{4}\left(\frac{a}{a+b}+\frac{a}{a+c}\right)\ge\frac{a}{a+1}\left(1\right)\)
Chứng minh tương tự, ta được:
\(\frac{1}{4}\left(\frac{b}{a+b}+\frac{b}{b+c}\right)\ge\frac{b}{b+1}\left(2\right)\);
\(\frac{1}{4}\left(\frac{c}{a+c}+\frac{c}{b+c}\right)\ge\frac{c}{c+1}\left(3\right)\)
Từ (1), (2), (3), ta được:
\(\frac{a}{a+1}+\frac{b}{b+1}+\frac{c}{c+1}\le\)\(\frac{1}{4}\left(\frac{a}{a+b}+\frac{a}{a+c}+\frac{b}{b+c}+\frac{b}{a+b}+\frac{c}{a+c}+\frac{c}{b+c}\right)\)
\(\Leftrightarrow P\le\frac{1}{4}\left[\left(\frac{a}{a+b}+\frac{b}{a+b}\right)+\left(\frac{b}{b+c}+\frac{c}{b+c}\right)+\left(\frac{c}{a+c}+\frac{a}{a+c}\right)\right]\)
\(\Leftrightarrow P\le\frac{1}{4}\left(\frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a}\right)\)
\(\Leftrightarrow P\le\frac{1}{4}\left(1+1+1\right)=\frac{1}{4}.3=\frac{3}{4}\)
Dấu bằng xảy ra.
\(\Leftrightarrow\hept{\begin{cases}a=b=c>0\\a+b+c=1\end{cases}}\Leftrightarrow a=b=c=\frac{1}{3}\)
Vậy \(maxP=\frac{3}{4}\Leftrightarrow a=b=c=\frac{1}{3}\)

.png)