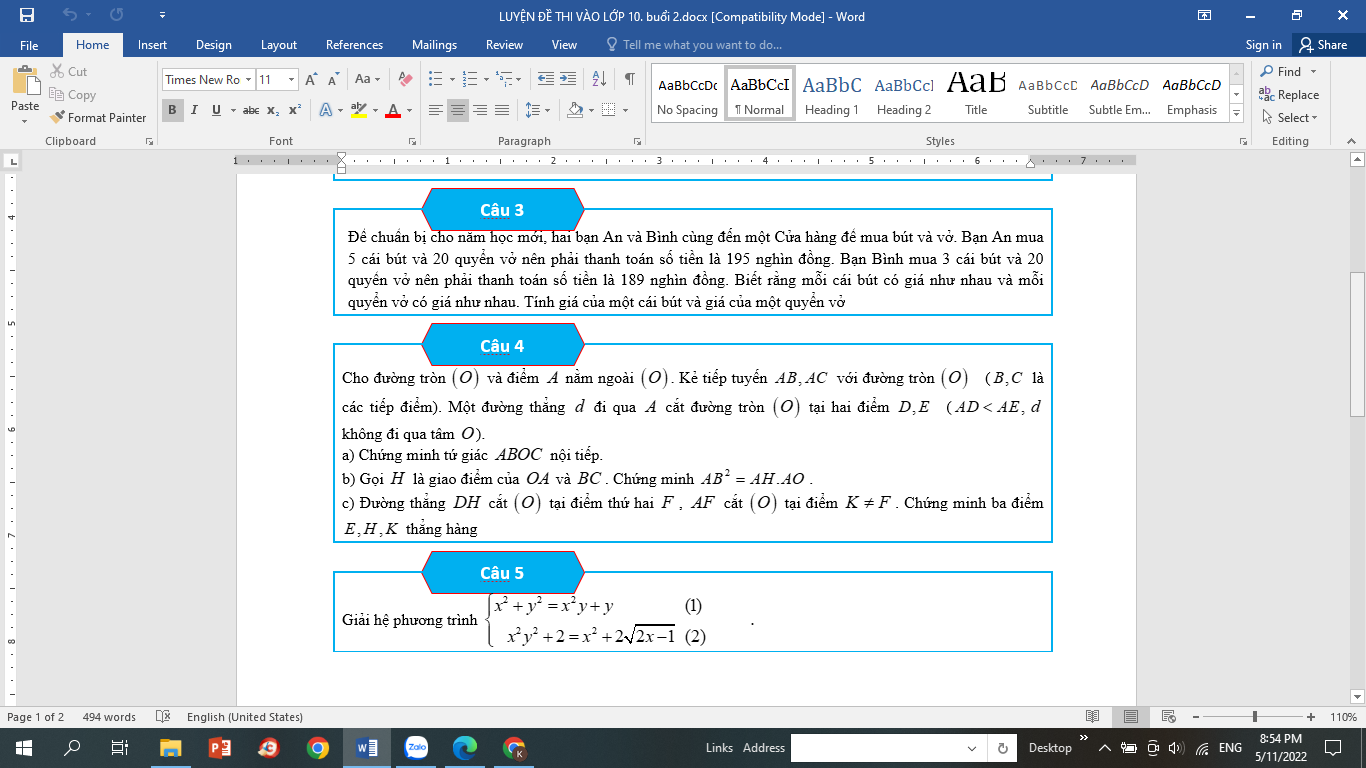
CÂU 4:
a) △ABC có (O) là tâm đường tròn nội tiếp và (O) tiếp xúc với AB,BC lần lượt tại D,E.
⇒OD⊥BC tại D, OE⊥AB tại E nên \(\widehat{ODB}=\widehat{OEB}=90^0\)
Tứ giác BDOE có \(\widehat{ODB}+\widehat{OEB}=90^0+90^0=180^0\)
\(\Rightarrow\)BDOE là tứ giác nội tiếp.
\(\Rightarrow\)B,D,O,E cùng thuộc 1 đường tròn.
b) Cách đơn giản nhất: *Gọi K là trung điểm BP.
Xét (O): BE, BD là 2 tiếp tuyến cắt nhau ở B.
\(\Rightarrow BE=BD\left(1\right)\)
PF, PE là 2 tiếp tuyến cắt nhau ở P.
\(\Rightarrow PF=PE\left(2\right)\)
Lấy (1)+(2) ta được \(BD+PF=BP\)
Ta có: DF⊥PQ tại F, DF⊥BC tại D nên PQ//BC.
Xét hình thang BDFP (BD//PF) có:
O là trung điểm DF, K là trung điểm BP.
\(\Rightarrow\)KO là đường trung bình của hình thang BDFP.
\(\Rightarrow KO=\dfrac{1}{2}\left(PF+BD\right)=\dfrac{1}{2}BP\)
Xét △BOP có: OK là trung tuyến và \(OK=\dfrac{1}{2}BP\)
\(\Rightarrow\)△BOP vuông tại O.
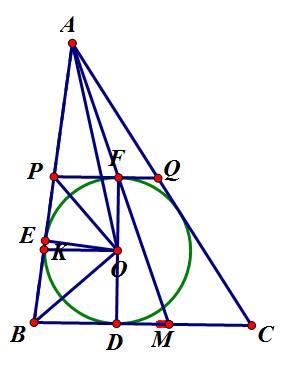
c) (O) tiếp xúc với AC tại H.
△ABC có (O) tiếp xúc với BC,AB,CA lần lượt tại D,E,H.
\(\Rightarrow BD=BE;AE=AH;CD=CH\)
\(BD+BE=AB-AE+BC-CD=AB+BC-AH-CH=AB+BC-AC\)
\(\Rightarrow BD=\dfrac{AB+BC-CA}{2}\left(3\right)\)
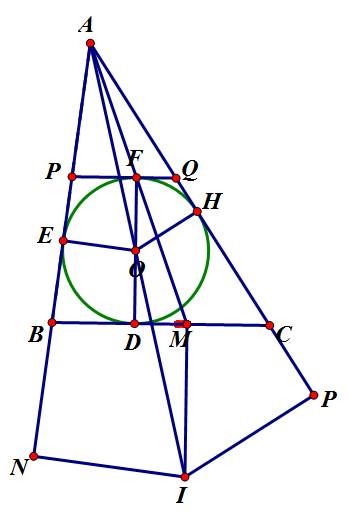
*Qua M kẻ đường thẳng vuông góc với BC cắt tia AO tại I.
*Hạ IN⊥AB tại N, IP⊥CA tại P.
Xét △AIM có: OF//IM \(\Rightarrow\dfrac{OF}{IM}=\dfrac{AO}{AI}\) (4) (hệ quả định lí Thales)
Xét △AIN có: OE//IN \(\Rightarrow\dfrac{OE}{IN}=\dfrac{AO}{AI}\) (5) (hệ quả định lí Thales)
Ta cũng có \(OE=OF\left(6\right)\) (bằng bán kính của (O) )
\(\left(4\right),\left(5\right),\left(6\right)\Rightarrow IM=IN\)
Dễ dàng chứng minh △BNI=△BMI (ch-cgv) nên \(\widehat{NBI}=\widehat{MBI}\)
\(\Rightarrow BI\) là phân giác của góc NBC hay BI là phân giác ngoài của △ABC.
Xét △ABC có: Phân giác trong góc A (AO) cắt phân giác ngoài góc B (BI) tại I.
\(\Rightarrow\)I là tâm đường tròn bàng tiếp ở đỉnh A.
Lại có IN⊥AB tại N, IM⊥BC tại M, IP⊥AC tại P.
\(\Rightarrow\)IN,IP,IM là các bán kính của (I).
\(\Rightarrow\)(I) tiếp xúc với AB,BC,CA lần lượt tại N,M,P.
\(\Rightarrow AN=AP;BN=BM;CM=CP\)
\(CM+CP=BC-BM+AP-AC=BC-AC+AN-BN=BC-AC+AB\)
\(\Rightarrow CM=\dfrac{BC+AB-AC}{2}\left(7\right)\)
\(\left(3\right),\left(7\right)\Rightarrow BD=CM\)

 GIẢI GIÚP MÌNH CÂU 4 CẢM ƠN Ạ :3
GIẢI GIÚP MÌNH CÂU 4 CẢM ƠN Ạ :3





 Ai giúp mình giải câu 3 với,mình cảm ơn nhìuuuu ạ 🥺
Ai giúp mình giải câu 3 với,mình cảm ơn nhìuuuu ạ 🥺
 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn




 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!