Question

Giải các phương trình |2x + 5| = x2 + 5x + 1

Answer 1

|2x + 5| = x2 + 5x + 1 (4)

Tập xác định: D = R.

+ Xét 2x + 5 ≥ 0 ⇔ 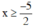 , khi đó |2x + 5| = 2x + 5

Khi đó pt (4) ⇔ 2x + 5 = x2 + 5x + 1

⇔ x2 + 3x – 4 = 0

⇔ (x + 4)(x – 1) = 0

⇔ x = –4 (không thỏa mãn) hoặc x = 1 (thỏa mãn)

+ Xét 2x + 5 < 0 ⇔ 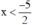 , khi đó |2x + 5| = –2x – 5.

Khi đó pt (4) ⇔ –2x – 5 = x2 + 5x + 1

⇔ x2 + 7x + 6 = 0

⇔ (x + 1)(x + 6) = 0

⇔ x = –1 (không thỏa mãn) hoặc x = –6 (thỏa mãn).

Vậy phương trình có hai nghiệm x = 1 hoặc x = –6.