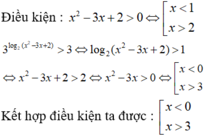Các câu hỏi tương tự
Giải các bất phương trình sau:a) (2x − 7)ln(x + 1) 0;b) (x − 5)(logx + 1) 0;c) 2
log
3
2
x
+ 5
log
2
2
x
+
log
2
x
– 2 ≥ 0d) ln(3
e
x
− 2) ≤ 2x
Đọc tiếp
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
Nghiệm của phương trình
log
4
2
log
3
1
+
log
2
1
+...
Đọc tiếp
Nghiệm của phương trình log 4 2 log 3 1 + log 2 1 + 3 log 2 x = 1/2 là
A. x = 1 B. x = 2
C. x = 3 D. x = 0
Nghiệm của phương trình log 4 { 2 log 3 [ 1 + log 2 ( 1 + 3 log 2 x ) ] } = 1/2 là
A. x = 1 B. x = 2
C. x = 3 D. x = 0
Tìm tập nghiệm của bất phương trình: 2 2 x 8 > 1
A. x > 3/2 B. x < 3/2
C. x > 2/3 D. x < 2/3
Tiệm cận đứng của đồ thị hàm số sau là:
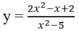
A. x = 2 B. x = 5 hoặc x = - 5
C. x = 1 hoặc x = -1 D. x = 3
Tiệm cận đứng của đồ thị hàm số sau là:
y
2
x
2
-
x
+
2
x
2
-
5
A. x 2 B. x...
Đọc tiếp
Tiệm cận đứng của đồ thị hàm số sau là:
y = 2 x 2 - x + 2 x 2 - 5
A. x = 2 B. x = 5 hoặc x = - 5
C. x = 1 hoặc x = -1 D. x = 3
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Xác định giá trị của tham số m để hàm số sau không có cực trịy m
x
3
/3 + m
x
2
+ 2(m - 1)x - 2.A. m
≤
0 hoặc m
≥
2 B. m
≥
0C. m
≤
0
≤
2 D. m ∈ [0; +
∞
]
Đọc tiếp
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Cho hàm số
y
x
3
-
2
x
2
-
1
(1) và các mệnh đề(1) Điểm cực trị của hàm số (1) là x 0 hoặc x 4/3(2) Điểm cực trị của hàm số (1) là x 0 và x 4/3(3) Điểm cực trị của đồ thị hàm số (1) là x 0 và x 4/3(4) Cực trị của hàm số (1) là x 0 và x 4/3Trong các mệnh đề trên, số mệnh đề sai là: A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Cho hàm số y = x 3 - 2 x 2 - 1 (1) và các mệnh đề
(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3
(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3
(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3
(4) Cực trị của hàm số (1) là x = 0 và x = 4/3
Trong các mệnh đề trên, số mệnh đề sai là:
A. 0
B. 1
C. 2
D. 3
Giải bất phương trình 2 x + 2 - x - 3 < 0 .