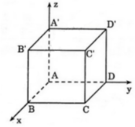
Đặt hình lập phương ABCD.A'B'C'D' vào hệ trục Oxyz sao cho O(0;0;0) ≡ A
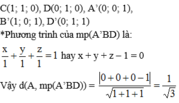
*mp(B'D'C')//mp(A'BD) vì (B'C//A'D và D'C//A'B) nên pt của mp (B'D'C) có dạng x+y+z+D=0 (D ≠ -1)
mp(B'D'C) đi qua điểm C(1;1;0) <=>D=-2
Suy ra pt của mp(B'D'C) là: x+y+z-z=0
![]()

Đặt hình lập phương ABCD.A'B'C'D' vào hệ trục Oxyz sao cho O(0;0;0) ≡ A
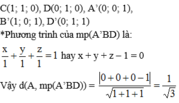
*mp(B'D'C')//mp(A'BD) vì (B'C//A'D và D'C//A'B) nên pt của mp (B'D'C) có dạng x+y+z+D=0 (D ≠ -1)
mp(B'D'C) đi qua điểm C(1;1;0) <=>D=-2
Suy ra pt của mp(B'D'C) là: x+y+z-z=0
![]()
giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Tính khoảng cách giữa hai mặt phẳng nói trên.
giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Chứng minh hai mặt phẳng (AB'D') và (BC'D) song song.
Bài 1. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 4. a. Tính độ dài đường chéo của hình lập phương. b. Tính góc giữa AC' và mặt đáy c. Tính góc giữa AC và B'C' d. Tính khoảng cách từ A đến (A'BD)
Mọi người cho em hỏi là bài toán Cho hình lập phương ABCD.A'B'C'D' có AB =a .Gọi O là tâm của hình vuông ABCD .Tính khoảng cách giữa 2 đường A'O và BC Bài này muốn giải bằng phương pháp trục tọa độ thì làm sao ạ
Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng 1. Dùng phương pháp tọa độ để: Tính khoảng cách giữa hai mặt phẳng đó.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi I là điểm thuộc cạnh AB sao cho AI=a. Tính khoảng cách từ điểm C đến mặt phẳng (B'DI).
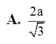
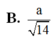
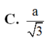
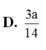
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ các đỉnh A(0;0;0), B(1;0;0), C(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADD'A' Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
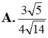
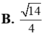
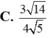
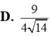
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ A(1;2;1), C(3;6;-3). Gọi M là một điểm bất kỳ thuộc mặt cầu ( S ) : x - 2 2 + y - 4 2 + z + 1 2 = 1 . Tính tổng các khoảng cách từ điểm M đến tất cả các mặt của hình lập phương ABCD.A'B'C'D'.
A. 2 3
B. 3 3
C. 6 3
D. 12
Cho hình lập phương ABCD.A'B'C'D' có tất cả các cạnh bằng 2. Khoảng cách giữa hai mặt phẳng (AB'D') và (BC'D') bằng:
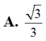
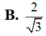

![]()