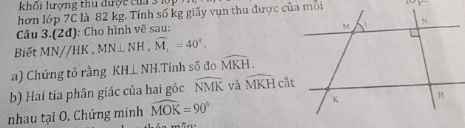Hình 82: Xét tam giác ADB và tam giác ADE có:
AB=AE (do giả thiết)
Â1=Â2
AD là cạnh chung
=> tam giác ADE = tam giác ADB (c.g.c)
Hình 83: Xét tam giác HGK và tam giác IKG có:
HG = IK (do giả thiết)
Góc G = góc K
GK là cạnh chung
=> tam giác HGK = tam giác IKG (c.g.c)
Hình 84: Xét tam giác PMQ và tam giác PMN có:
Góc M1 = góc M2
PM là cạnh chung
NP = QP
Nhưng góc M không phải là góc xen giữa nên:
=> tam giác PMQ không bằng tam giác PMN.
Học tốt nhé bạn để sau này thành Einsten thứ 3 nhen.
Lời giải chi tiết
Hình 82
Xét ΔADB∆ADB và ΔADE∆ADE có:
+) AB=AEAB=AE (giả thiết)
+) ˆA1=ˆA2A1^=A2^ (giả thiết)
+) ADAD chung
⇒ΔADB=ΔADE(c.g.c)⇒∆ADB=∆ADE(c.g.c)
Hình 83
Xét ΔHGK∆HGK và ΔIKG∆IKG có:
+) HG=IKHG=IK (giả thiết)
+) ˆHGK=ˆIKGHGK^=IKG^ (giả thiết)
+) GKGK là cạnh chung
⇒ΔHGK=ΔIKG(c.g.c)⇒∆HGK=∆IKG(c.g.c)
Hình 84
Xét ΔPMQ∆PMQ và ΔPMN∆PMN có:
MPMP cạnh chung
ˆM1=ˆM2M1^=M2^ (giả thiết)
PQ=PNPQ=PN (giả thiết)
Nhưng ˆM1M1^ không xen giữa hai cạnh MPMP và PNPN
ˆM2M2^ không xen giữa hai cạnh MPMP và PQPQ
Nên ΔPMQΔPMQ không bằng ΔPMNΔPMN.
chúc bạn học tốt
tick nha