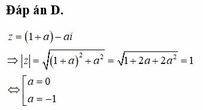Các câu hỏi tương tự
Cho số phức za+bi (
a
,
b
∈
R
) thỏa mãn
z
+
1
+
2
i
-
(
1
+
i
)
z
0
;
z
1
. Tính giá trị của biểu thức Pa+b.
Đọc tiếp
Cho số phức z=a+bi ( a , b ∈ R ) thỏa mãn z + 1 + 2 i - ( 1 + i ) z = 0 ; z > 1 . Tính giá trị của biểu thức P=a+b.
Cho số phức
z
a
+
b
i
(
a
,
b
∈
ℝ
;
a
≥
0
;
≥
0
)
. Đặt đa thức
f
(
x
)
a
x
2
+
b
x...
Đọc tiếp
Cho số phức z = a + b i ( a , b ∈ ℝ ; a ≥ 0 ; ≥ 0 ) .
Đặt đa thức f ( x ) = a x 2 + b x - 2 .
Biết f ( - 1 ) ≤ 0 , f ( 1 4 ) ≤ - 5 4 .
Tìm giá trị lớn nhất của z
A. max z = 2 5
B. max z = 3 2
C. max z = 5
D. max z = 2 6
Cho số phức
z
a
+
b
i
khác 0. Số phức
z
-
1
có phần thực là
Đọc tiếp
Cho số phức z = a + b i khác 0. Số phức z - 1 có phần thực là
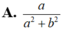
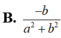
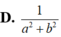
Cho số phức z a + bi
0
≤
a
≤
4
;
b
≥
0
. Đặt hàm số
f
(
x
)
a
x
2
+
b
x
+
2
. Biết
f
1
4
≤
-
5...
Đọc tiếp
Cho số phức z = a + bi 0 ≤ a ≤ 4 ; b ≥ 0 . Đặt hàm số f ( x ) = a x 2 + b x + 2 . Biết f 1 4 ≤ - 5 4 . Giá trị lớn nhất của z thuộc khoảng nào dưới đây
A. (4; 4,3)
B. (4,3 ; 4,5)
C. (4,5 ; 4,7)
D. (4,7; 5)
Cho số phức z a +bi (a,b là các số thực) thỏa mãn
z
.
z
+
2
z
+
i
0
Tính giá trị của biểu thức
T
a
+
b
2
Đọc tiếp
Cho số phức z = a +bi (a,b là các số thực) thỏa mãn z . z + 2 z + i = 0 Tính giá trị của biểu thức T = a + b 2
Cho số phức za+bi (a,b là các số thực) thỏa mãn
z
.
z
¯
+
2
z
+
i
0
. Tính giá trị của biểu thức T
a
+
b
2
A. T
4...
Đọc tiếp
Cho số phức z=a+bi (a,b là các số thực) thỏa mãn z . z ¯ + 2 z + i = 0 .
Tính giá trị của biểu thức T= a + b 2
A. T= 4 3 - 2
B. T= 3 + 2 2
C. T= 3 - 2 2
D. T= 4 + 2 3
Cho phương trình 8z2 - 4(a + 1)z + 4a + 1 0 (1) với a là tham số. Tính tổng tất cả các giá trị của a để (1) có hai nghiệm z1; z2 thỏa mãn z1/ z2 là số ảo, trong đó z2 là số phức có phần ảo dương. A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho phương trình 8z2 - 4(a + 1)z + 4a + 1 = 0 (1) với a là tham số. Tính tổng tất cả các giá trị của a để (1) có hai nghiệm z1; z2 thỏa mãn z1/ z2 là số ảo, trong đó z2 là số phức có phần ảo dương.
A. 1
B. 2
C. 3
D. 4
Cho z = a + bi ∈ C, biết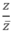 
là một số thuần ảo. Kết luận nào sau đây là đúng?
A. a = 0 B. b = 0
C. a = b D. a = b hoặc a = -b
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7