Các câu hỏi tương tự
mọi người cho em hỏi là thi vào 10 có được dùng các bất đẳng thức như cauchy mà ko cần chứng minh không ạ?
các bạn cho mình hỏi là có bất đẳng thức nào kiểu như xy >= z (z là một biểu thức chứa x và y) không ạ ?
Chứng minh bất đẳng thức Cô-si với n số không âm.
1) chứng minh bất đẳng thức Bu-nhi-a-cốp-ski với bộ n số.
Ai nhanh mình tick!^_^
bạn nào có hiểu bít về bất đẳng thức bunhia coopsxki cho tớ bit vs
Cho hai số a, b, không âm. Chứng minh: a + b 2 ≥ a b (Bất đẳng thức Cô-si cho hai số không âm). Dấu đẳng thức xảy ra khi nào?
Tìm hằng số \(M\) nhỏ nhất để bất đẳng thức sau đúng với mọi \(x,y,z\) không âm:
\(1-xy-yz-zx\le M\left(1-min\left\{x,y,z\right\}\right)\)
P/S: Bài này khá dễ, vì bất đẳng thức này lỏng. Không biết có "cao thủ" nào làm chặt được bất đẳng thức này không ha.
Với x,y,z dương. Không sử dụng bất đẳng thức Cosi. C/m biểu thức sau
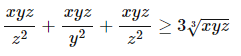
Giúp em với ạ, em đang cần gấp ạ! Em cảm ơn nhiều!
Chứng minh bất đẳng thức sau:
a, 1/a <1/b
b, a^2 + ab + b^2>= 0
Chứng minh:
x
3
+
y
3
+
z
3
-
3
x
y
z
1
/
2
.
x
+...
Đọc tiếp
Chứng minh: x 3 + y 3 + z 3 - 3 x y z = 1 / 2 . x + y + z x - y 2 + y - z 2 + z - x 2
Từ đó chứng tỏ: Với ba số a, b, c không âm thì x 3 + y 3 + z 3 3 ≥ x y z
(Bất đẳng thức Cô-si cho ba số không âm)
Dấu đẳng thức xảy ra khi ba số a, b, c bằng nhau.
Chứng minh bất đẳng thức nesbitt
Nếu a,b,c là các số dương ta có \(P=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{b+a}\ge\frac{3}{2}\)
Chứng minh giúp em dễ hiểu vs ạ

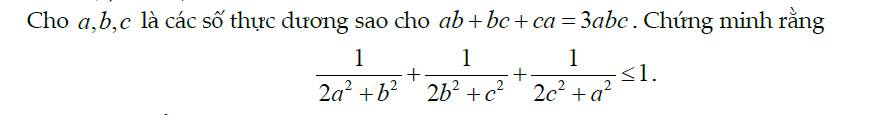
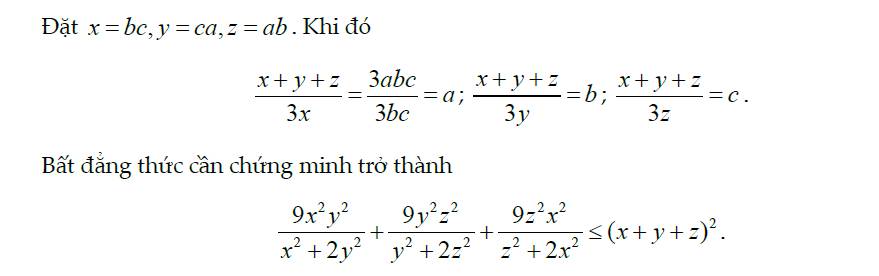 Em không hiểu cách chuyển từ bất đẳng thức gốc sang bất đẳng thức mới ạ
Em không hiểu cách chuyển từ bất đẳng thức gốc sang bất đẳng thức mới ạ









