Phân tích:
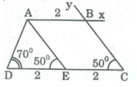
Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán. Qua A kẻ đường thẳng song song với BC cắt CD tại E. Hình thang ABCE có 2 cạnh bên song song nên AB = EC = 2cm do đó DE = 2cm
Tam giác ADE dựng được vì biết 2 góc kề với một cạnh.
Điểm C nằm trên tia DE cách D một khoảng bằng 4cm.
Điểm B thỏa mãn hai điều kiện:
- B nằm trên đường thẳng đi qua A và song song với CD.
- B nằm trên đường thẳng đi qua C và song song với AE.
Cách dựng:
- Dựng ΔADE biết DE = 2cm, ∠ D = 70 0 , ∠ E = 50 0
- Trên tia DE lấy điểm C sao cho DC = 4cm
- Dựng tia Ax // CD, Ax nằm trên nửa mặt phẳng bờ AD chứa điểm C
- Dựng tia Cy // AE, Cy nằm trên nửa mặt phẳng bờ CD chứa điểm A.
Cy cắt Ax tại B. Hình thang ABCD cần dựng.
Chứng minh:
Tứ giác ABCD là hình thang vì AB // CD.
CD = CE + ED ⇒ CE = CD – ED = 4 – 2 = 2 (cm)
Hình thang ABCE có hai cạnh bên AE // CB
⇒ AB = CE = 2 (cm)
∠ C = ∠ E = 50 0 (hai góc đồng vị)
∠ D = 70 0
Hình thang ABCD thỏa mãn điều kiện bài toán.
Biện luận: Tam giác ADE luôn dựng được, hình thang ABCD luôn dựng được. Ta dựng được một hình thang thỏa mãn điều kiện bài toán.