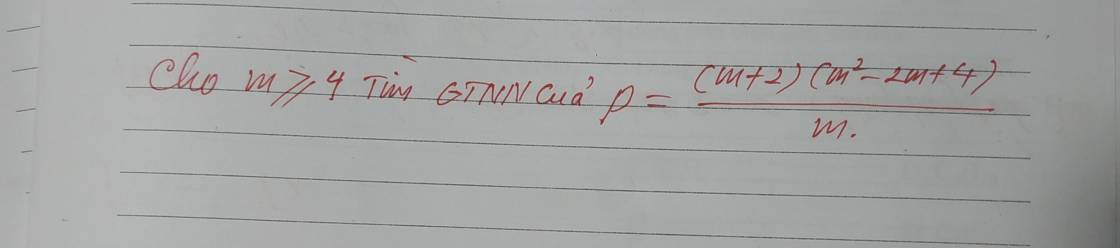`P=((m+2)(m^2-2m+4))/m`
`=(m^3+8)/m`
`=m^2+8/m`
`=(m^2+64/m+64/m)-120/m`
Theo BĐT côsi cho ba số dương `m^2;64/m;64/m` ta có:
`m^2+64/m+64/m >= 3\root[3]{m^2 . 64/m . 64/m}=48(1)`
Mặt khác: `m>=4` nên `120/m<=30 =>-120/m>=-30(2)`
Cộng hai vế của `(1)` và `(2)` có `P>=48-30=18`
Dấu "=" xảy ra `<=>{(m^2=64/m),(m=4):}<=>m=4`
Vậy `P_(min)=18<=>m=4`
Cho a+b=1 ; a;b>0
Tim min A;A=\(\frac{1}{ab}+\frac{1}{a^2+b^2}\)
(goi y tach 2 pthuc thanh 3 pthuc ; su dung bdt cosi+svacxo)
Ad bđt cosi để cm :
a/b+c + b/c+a + c/a+b > 3/2
Mn giải từng bc hộ e ạ :33 Tại e mới học cosi !!
chung minh bat dang thuc cosi
Cho x, y>0 và xy = 1. Tìm giá trị nhỏ nhất của
M = x2 + y2 + 3/(x+y+1)
Bài này ngoài cosi ra giúp mình giải cách khâc với. Nhất là cách lớp 8 ý, thầy mình ko cho dùng cosi
Cho x,y,z,a,b,c>0.CMR:\(\sqrt[3]{abc}+\sqrt[3]{xyz}\le\sqrt[3]{\left(a+x\right)\left(b+y\right)\left(c+z\right)}\)
Áp dụng bđt cosi nha!!! thank nhìu!! Sẽ tick cho bn nhanh và đúng nhất! :))))
áp dụng bdt cosi tìm gtnn của y=3x/2+1/x+1;x>-1
áp dụng bdt cosi tìm gtnn của y=x/3+5/2x-1; x>1/2
áp dụng bdt cosi tìm gtln của y= (x+3)(5-2x); -3<=x<=5/2
áp dụng bdt cosi tìm gtnn của y=x/1-x+5/x; 0<x<1
