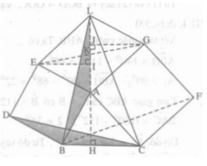
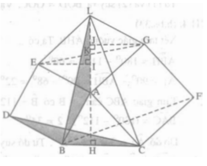
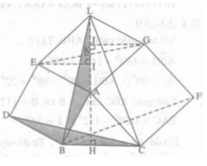
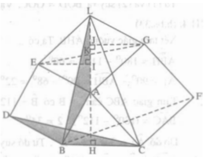
Xét tam giác ALB và ∆BCD có:
AL = BC ( chứng minh b)
AB = BD ( vì ABDE là hình vuông)
∠(BAL) = 90º + ∠(EAL) = 90 + ∠(ABC) = ∠(DBC) .
Suy ra: ∆ALB = ∆BCD ( c.g.c)
Suy ra ∠(ALB) = ∠(BCD) .
Mặt khác ta có ∠(ALB) + ∠(LBH) = 90º nên ∠(BCD) + ∠(LBH) = 90º.
Suy ra LB ⊥ CD, tức CD là một đường cao của tam giác LBC.