- Giả thiết : ΔABC có I là giao điểm ba đường phân giác
IH, IK, IL lần lượt là khoảng cách từ I đến BC, AC, AB
- Kết luận : IH = IK = IL
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
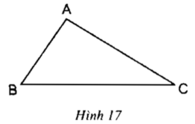
Dựa vào hình 17, hãy viết giả thiết, kết luận của định lý
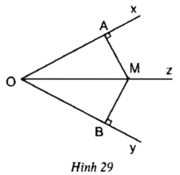
Dựa vào hình 29, hãy viết giả thiết và kết luận của định lí 1.
Em hãy vẽ hình, viết giả thiết, kết luận và chứng minh định lý trên.
Vẽ hình và viết giả thiết, kết luận của định lý (viết bằng ký hiệu ) "Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau".Vẽ hình và viết giả thiết, kết luận của định lý (viết bằng ký hiệu ) "Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau"
C1 Phát biểu định lý diễn tả bằng hình vẽ sau.Viết giả thiết và kết luận của định lý đó bằng ký hiệu?
Nếu hai đường thẳng xx’ , yy’ cắt nhau tại O và góc xOy vuông thì các góc x’Oy’ ; yOx’ ; xOy’ đều là góc vuông.”
a. Hãy vẽ hình theo định lý
b. Viết giả thiết và kết luận của định lý .
Chọn định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là: A. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OE ⊥ OF B. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOF, OF là phân giác góc AOD. Kết luận: OE ⊥ OA C. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOE. Kết luận: OE ⊥ OF D. Giả thiết: Cho góc bẹt AOB và tia OD, OE là...
Đọc tiếp
Chọn định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
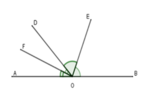
A. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OE ⊥ OF
B. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOF, OF là phân giác góc AOD. Kết luận: OE ⊥ OA
C. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOE. Kết luận: OE ⊥ OF
D. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OB ⊥ OF
Hãy vẽ hình minh họa và giả thiết, kết luận cho định lý: "Nếu 1 đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì nó cũng vuông góc với đường thẳng kia".
Hãy vẽ hình minh họa và ghi giả thiết , kết luận bằng kí hiệu của định lý sau : " hai đường thẳng phân biệt cùng vuông góc với 1 đường thẳng thứ ba thì chúng song song với nhau "