0,5x(x + 1) = (x – 1)2
⇔ 0,5x2 + 0,5x = x2 – 2x + 1
⇔ x2 – 2x + 1 – 0,5x2 – 0,5x = 0
⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0
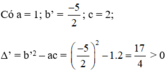
Phương trình có hai nghiệm phân biệt:
0,5x(x + 1) = (x – 1)2
⇔ 0,5x2 + 0,5x = x2 – 2x + 1
⇔ x2 – 2x + 1 – 0,5x2 – 0,5x = 0
⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0
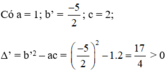
Phương trình có hai nghiệm phân biệt:
Đưa các phương trình sau về dạng ax2 + 2b'x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):
3x2 + 3 = 2(x + 1)
Đưa các phương trình sau về dạng ax2 + 2b'x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):
(2x - √2)2 – 1 = (x + 1)(x – 1)
Đưa các phương trình sau về dạng a x 2 + 2 b ' x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):
a ) 3 x 2 − 2 x = x 2 + 3 b ( 2 x - 2 ) − 1 = ( x + 1 ) ( x − 1 ) c ) 3 x 2 + 3 = 2 ( x + 1 ) d ) 0 , 5 x ( x + 1 ) = x - 1 2
Đưa các phương trình sau về dạng ax2 + 2b'x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):
3x2 – 2x = x2 + 3
Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương tình sau (làm tròn đến chữ số thập phân thứ ba):
a ) x 2 = 2 ; b ) x 2 = 3 c ) x 2 = 3 , 5 ; d ) x 2 = 4 , 12
Hướng dẫn: Nghiệm của phương trình x 2 = a ( với a ≥ 0) là các căn bậc hai của a.
Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương tình sau (làm tròn đến chữ số thập phân thứ ba):
x2 = 2
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư): cotg25o18'
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư): tg63o36'
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư):
cos52o54'