Em học lớp 6 em ko biết trả lời
Các câu hỏi tương tự
Cho đường tròn (O;R) đường kính AB. Gọi H là một điểm bất kỳ trên đoạn OA (H khác hai điểm O, A). Dựng đường thẳng d vuông góc với OA tại H. Trên d lấy điểm C ở ngoài đường tròn (O). Kẻ các tiếp tuyến CM, CN với đường tròn (O); M và N là tiếp điểm, M cùng phía với A bờ CH. Các đường thẳng CM, CN cắt đường thẳng AB tại P và Q. Đường thẳng qua O và vuông góc với AB cắt MN tại K. CK cắt AB tại I. Chứng minh rằng: 1) HC là tia phân giác của góc MHN 2) I là trung điểm của đoạn thẳng PQ 3) Ba đường th...
Đọc tiếp
Cho đường tròn (O;R) đường kính AB. Gọi H là một điểm bất kỳ trên đoạn OA (H khác hai điểm O, A). Dựng đường thẳng d vuông góc với OA tại H. Trên d lấy điểm C ở ngoài đường tròn (O). Kẻ các tiếp tuyến CM, CN với đường tròn (O); M và N là tiếp điểm, M cùng phía với A bờ CH. Các đường thẳng CM, CN cắt đường thẳng AB tại P và Q. Đường thẳng qua O và vuông góc với AB cắt MN tại K. CK cắt AB tại I. Chứng minh rằng: 1) HC là tia phân giác của góc MHN 2) I là trung điểm của đoạn thẳng PQ 3) Ba đường thẳng PN, QM và CH đồng quy.
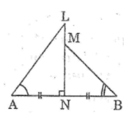
CHO TAM GIÁC ABC CÂN TẠI A,TRÊN ĐƯỜNG THẲNG VUÔNG GÓC VỚI AC TẠI C LẤY ĐIỂM D BẤT KỲ (B,D KHÁC PHÍA SO VỚI AC).GỌI K LÀ GIAO ĐIỂM CỦA ĐƯỜNG THẲNG QUA B VUÔNG GÓC VỚI AB VÀ ĐƯỜNG THẲNG QUA TRUNG ĐIỂM M CỦA CD VUÔNG GÓC VỚI AD. SO SÁNH CB VÀ KD
CHO TAM GIÁC ABC CÂN TẠI A,TRÊN ĐƯỜNG THẲNG VUÔNG GÓC VỚI AC TẠI C LẤY ĐIỂM D BẤT KỲ (B,D KHÁC PHÍA SO VỚI AC).GỌI K LÀ GIAO ĐIỂM CỦA ĐƯỜNG THẲNG QUA B VUÔNG GÓC VỚI AB VÀ ĐƯỜNG THẲNG QUA TRUNG ĐIỂM M CỦA CD VUÔNG GÓC VỚI AD. SO SÁNH CB VÀ KD
CHO TAM GIÁC ABC CÂN TẠI A,TRÊN ĐƯỜNG THẲNG VUÔNG GÓC VỚI AC TẠI C LẤY ĐIỂM D BẤT KỲ (B,D KHÁC PHÍA SO VỚI AC).GỌI K LÀ GIAO ĐIỂM CỦA ĐƯỜNG THẲNG QUA B VUÔNG GÓC VỚI AB VÀ ĐƯỜNG THẲNG QUA TRUNG ĐIỂM M CỦA CD VUÔNG GÓC VỚI AD. SO SÁNH CB VÀ KD
cho đoạn thẳng AC và đường thẳng d vuông góc với AC tại C. trên đoạn thẳng d vuông góc vs AC tại C,trên đoạn thẳng AC lấy B sao cho AB<AC vẽ đường tròn đường kính AB. gọi M là điểm trên cung góc AB. đường thẳng AM cắt d tại H
CM: tứ giác BCHM nội tiếp,so sánh góc BMC và BHC
Cho đường tròn ( O; R ) đường kính AB . trên tia AB lấy điểm C bằm ngoài đường tròn . kẻ đường thẳng d vuông góc với AB tại C. Gọi E là trung điểm của đoạn thẳng OB , đường thẳng đi qua E cắt đường tròn (O) ở M và N ( M khác A và B ) . Tia AM . AN thứ tự cắt d ở P và Q
1. Chứng minh tứ giác BCPM nội tiếp
cho tam giác ABC vuông tại A, gọi D là trung điểm của cạnh BC.Lấy điểm M bất kì trên đoạn thẳng AD(M không trùng với A).Gọi N,P theo thứ tự là hình chiếu vuông góc của M xuống AB,AC và H la hình chiếu vuông góc của N xuống đường thẳng PD .a) Chứng minh AH vuông góc với BH.b) Đường thẳng qua B song song với AD cắt đường trung trực của AB tại I chứng minh ba điểm H,N,I thẳng hàng
Đọc tiếp
cho tam giác ABC vuông tại A, gọi D là trung điểm của cạnh BC.Lấy điểm M bất kì trên đoạn thẳng AD(M không trùng với A).Gọi N,P theo thứ tự là hình chiếu vuông góc của M xuống AB,AC và H la hình chiếu vuông góc của N xuống đường thẳng PD .
a) Chứng minh AH vuông góc với BH.
b) Đường thẳng qua B song song với AD cắt đường trung trực của AB tại I
chứng minh ba điểm H,N,I thẳng hàng
cho đường tròn ( O;R) có đường kính AB , một điểm C nằm trên ( O;R) khác A và khác B. Vẽ đường thẳng d vuông góc với AB tại A. Đường thẳng BC cắt d tại D. Gọi M là trung điểm của AD.
1) Nếu biết góc CBA= 60 độ và R=3cm, hãy tìm độ dài các đoạn thẳng BD và MO
2) Chứng minh MC là tiếp tuyến của đường tròn ( O;R)
Cho tam giác ABC vuông tại A. M Là điểm di động trên cạnh AB. Đường thẳng qua M vuông góc với BC tại D cắt AC tại N. Gọi E,F lần lượt là trung điểm của các đoạn thẳng BM và CN.
Chứng minh trung điểm I của EF thuộc một đường cố định.