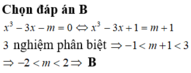Các câu hỏi tương tự
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
có đồ thị như hình bên. Tất cả các giá trị của m để phương trình
f
x
+
m
-
1
0
có 3 nghiệm phân biệt là: A. m1. B. m2. C. m...
Đọc tiếp
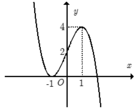
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị như hình bên. Tất cả các giá trị của m để phương trình f x + m - 1 = 0 có 3 nghiệm phân biệt là:

A. m=1.
B. m=2.
C. m= ± 1.
D. m=0.
Cho hàm số yf(x) liên tục trên
ℝ
,f(2)3 và có đồ thị như hình vẽ bên Có bao nhiêu số nguyên
m
∈
-
20
;
20
để phương trình có 4 nghiệm thực phân biệt.
f
(
x
+
m
)
3
A. 2 B. 18 C. 4 D. 19
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ ,f(2)=3 và có đồ thị như hình vẽ bên
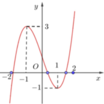
Có bao nhiêu số nguyên m ∈ - 20 ; 20 để phương trình có 4 nghiệm thực phân biệt. f ( x + m ) = 3
A. 2
B. 18
C. 4
D. 19
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
Tìm tất cả các giá trị thực của tham số m để phương trình
|
x
|
3
-
3
|
x
|
2
m
có 4 nghiệm phân biệt A. B. C. D.
Đọc tiếp
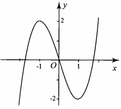
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình | x | 3 - 3 | x | = 2 m có 4 nghiệm phân biệt
A.![]()
B. ![]()
C.![]()
D. ![]()
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
Tìm tất cả các giá trị thực của tham số m để phương trình
64
|
x
|
3
(
x
2
+
1
)
2
(
12
|
x
|
+
m
(
x
2
+
1
)
)...
Đọc tiếp
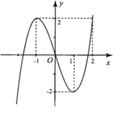
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình 64 | x | 3 = ( x 2 + 1 ) 2 ( 12 | x | + m ( x 2 + 1 ) ) có nghiệm.
A.![]()
B. Với mọi m
C. ![]()
D. ![]()
Cho hàm số yf(x) có đạo hàm trên
ℝ
. Đồ thị hàm số yf(x) như hình vẽ bên dưới Tìm m để bất phương trình
m
-
x
≥
2
f
x
+
2
+
4
x
+
3
nghiệm đúng với mọi
x
∈
-
3
;...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị hàm số y=f'(x) như hình vẽ bên dưới
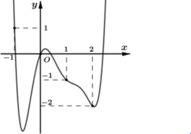
Tìm m để bất phương trình m - x ≥ 2 f x + 2 + 4 x + 3 nghiệm đúng với mọi x ∈ - 3 ; + ∞
A. m ≥ 2 f ( 0 ) - 1
B. m ≤ 2 f ( 0 ) - 1
C. m ≤ 2 f ( - 1 )
D. m ≥ 2 f ( - 1 )
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Cho hàm số
y
f
(
x
)
a
x
4
+
b
x
2
+
c
(
a
≠
0
)
có đồ thị như hình bên. Tất cả các giá trị của m để phương trình
f
(
x
)
+
m
+
1
0...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 4 + b x 2 + c ( a ≠ 0 ) có đồ thị như hình bên. Tất cả các giá trị của m để phương trình f ( x ) + m + 1 = 0 có 7 nghiệm phân biệt là:
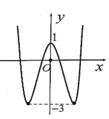
A. m=-2.
B. m=-1.
C. m=2.
D. m=0.
Cho hàm số yf(x) có đồ thị như hình vẽ. Tổng các giá trị nguyên m để phương trình f(f(x) +1) m có 3 nghiệm phân biệt bằng A. 15 B. 1 C. 13 D. 11
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ.
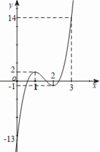
Tổng các giá trị nguyên m để phương trình
f(f(x) +1) = m có 3 nghiệm phân biệt bằng
A. 15
B. 1
C. 13
D. 11
Cho hàm số y f(x) xác định trên R và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình 2
f
(
x
)
- m 0 có đúng bốn nghiệm phân biệt. A. 0 m 8 B.m 4 C.m 0 ; m 8 D. -2 m 4
Đọc tiếp
Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình
2 f ( x ) - m = 0 có đúng bốn nghiệm phân biệt.
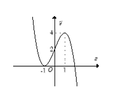
A. 0< m< 8
B.m> 4
C.m< 0 ; m> 8
D. -2< m< 4