Đáp án B.
Ta có: y’ = 12x3 – 12x2 – 12x + 12.
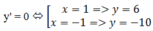
Bảng biến thiên
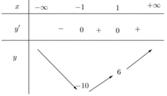
=> M(-1;-10) => x1 + y1 = -11
Đáp án B.
Ta có: y’ = 12x3 – 12x2 – 12x + 12.
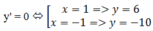
Bảng biến thiên

=> M(-1;-10) => x1 + y1 = -11
Đồ thị hàm số y = 3 x 4 - 4 x 3 - 6 x 2 + 12 x + 1 đạt cực tiểu tại điểm M (x1;y1). Tính tổng của T = x 1 + y 1
A. 3
B. -11
C. 8
D. 4
Đồ thị của hàm số y = 3x4 – 4x3 – 6x2 + 12x + 1 đạt cực tiểu tại M(x1; y1). Khi đó x1 + y1 bằng
A. 5
B. 6
C. -11
D. 7
Cho hàm số y = x 3 - 6 x 2 + 4 x - 7 . Gọi hoành độ 2 điểm cực trị của đồ thị hàm số là x 1 , x 2 . Khi đó, giá trị của tổng x 1 + x 2 là
A. -6
B. -4
C. 6
D. 4
Cho hàm số y = 1 3 x 4 - 14 3 x 2 có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt đồ thị ( C) tại hai điểm phân biệt M( x1; y1) và N( x2; y2) (M; N khác A) sao cho y2- y1= 8( x2- x1).
A. 0
B. 2
C. 3
D. 5
Cho đồ thị hàm số y = a x 4 + b x 2 + c
đạt cực đại tại A(0;3) và đạt cực tiểu tại B(1;-3). Tính giá trị của biểu thức P = a + 3b + 2c
A. -12
B. -24
C. -9
D. 0
Cho hàm số y = 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng?
A. (x1 – x2)2 = 8
B. x1x2 = 2
C. x2 – x1 = 3
D. x12 + x22 = 6
Đồ thị của hàm số ![]() đạt cực tiểu tại
đạt cực tiểu tại ![]() . Tính tổng
. Tính tổng ![]()
A. 5
B. - 11
C. - 7
D. 8
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn
Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có hai cực trị x 1 , x 2 thỏa - 2 < x 1 < 0 < x 2 < 2 và có đồ thị như hình vẽ.
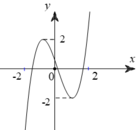
Số điểm cực tiểu của hàm số ![]() là
là
A. 3.
B. 5.
C. 7.
D. 4.