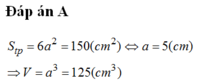Các câu hỏi tương tự
Cho khối lập phương ABCD.ABCD cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MBDN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:A.
a
3
9
B.
a
3
6
C.
a...
Đọc tiếp
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MB'D'N) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:
A. a 3 9 B. a 3 6
C. a 3 4 D. 7 a 3 24
Một hình lập phương có diện tích toàn phần là 150cm2. Thể tích của khối lập phương là
A. 125cm3
B. 216cm3
C. 81cm3
D. 64cm3
Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi
V
1
là thể tích khối chứa điểm A’ và
V
2
là thể tích khối chứa điểm C’. Khi đó
V
1
V
2
là A.
25
47...
Đọc tiếp
Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi V 1 là thể tích khối chứa điểm A’ và V 2 là thể tích khối chứa điểm C’. Khi đó V 1 V 2 là
A. 25 47 .
B. 1
C. 17 25 .
D. 8 17 .
Cho hình lập phương ABCD.ABCD có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông ABCD. Kết quả tính diện tích toàn phần của khối nón có dạng bằng
π
a
2
4
(
b
+
c
)
với b, c là hai số nguyên dương và
b
1
. Tính b.c.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A'B'C'D'. Kết quả tính diện tích toàn phần của khối nón có dạng bằng π a 2 4 ( b + c ) với b, c là hai số nguyên dương và b > 1 . Tính b.c.

![]()
![]()
![]()
Lập phương trình của mặt phẳng (α) đi qua điểm M(1; 2; 3) và cắt ba tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất.
Cho hình lập phương ABCD.ABCD cạnh a. Các điểm E và F lần lượt là trung điểm của CB và CD. Mặt phẳng ( AEF) cắt khối lập phương đã cho thành hai phần, gọi V1 là thể tích khối chứa điểm A và V2 là thể tích khối chứa điểm C’. Khi đó tỉ số
V
1
V
2
bằng A.
25
47
B. 1 C.
17
25...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Các điểm E và F lần lượt là trung điểm của C'B' và C'D'. Mặt phẳng ( AEF) cắt khối lập phương đã cho thành hai phần, gọi V1 là thể tích khối chứa điểm A' và V2 là thể tích khối chứa điểm C’. Khi đó tỉ số V 1 V 2 bằng
A. 25 47
B. 1
C. 17 25
D. 8 17
Tổng diện tích các mặt của một khối lập phương là
54
c
m
2
Tính thể tích của khối lập phương đó A.
27
c
m
3
B.
9
c
m
3
C.
81...
Đọc tiếp
Tổng diện tích các mặt của một khối lập phương là 54 c m 2 Tính thể tích của khối lập phương đó
A. 27 c m 3
B. 9 c m 3
C. 81 c m 3
D. 18 c m 3
Diện tích một mặt của hình lập phương là 9. Thể tích khối lập phương đó là:
A. 729.
B. 81.
C. 27.
D. 9.
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh
A
B
và sao cho
M
A
M
B
và
N
B
2
N
C
. Mặt phẳng
D
M...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh A ' B ' và sao cho M A ' = M B ' và N B = 2 N C . Mặt phẳng D M N chia khối lập phương đã cho thành hai khối đa diện. Gọi V H là thể tích khối đa diện chứa đỉnh A , V H ' là thể tích khối đa diện còn lại. Tỉ số V H V H ' bằng
A. 151 209
B. 209 360
C. 2348 3277
D. 151 360