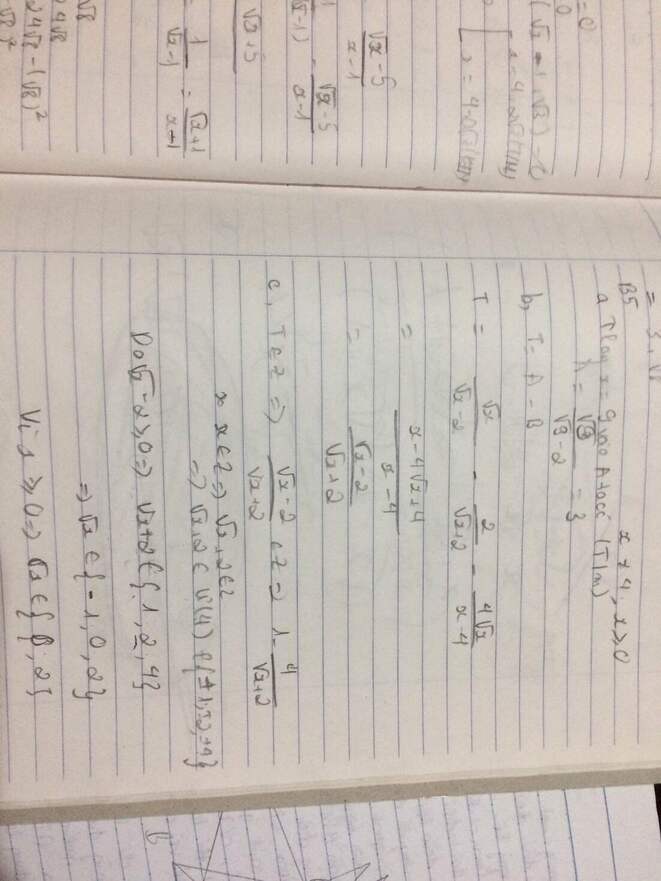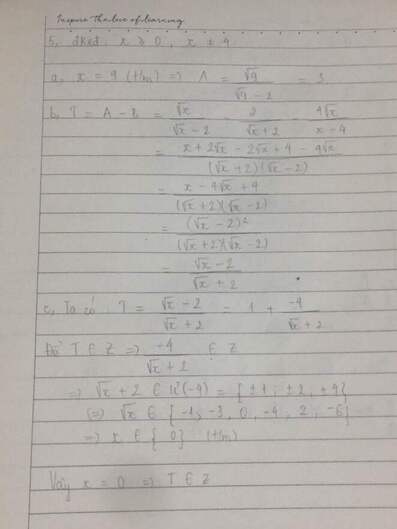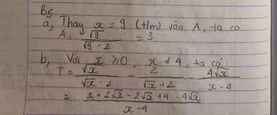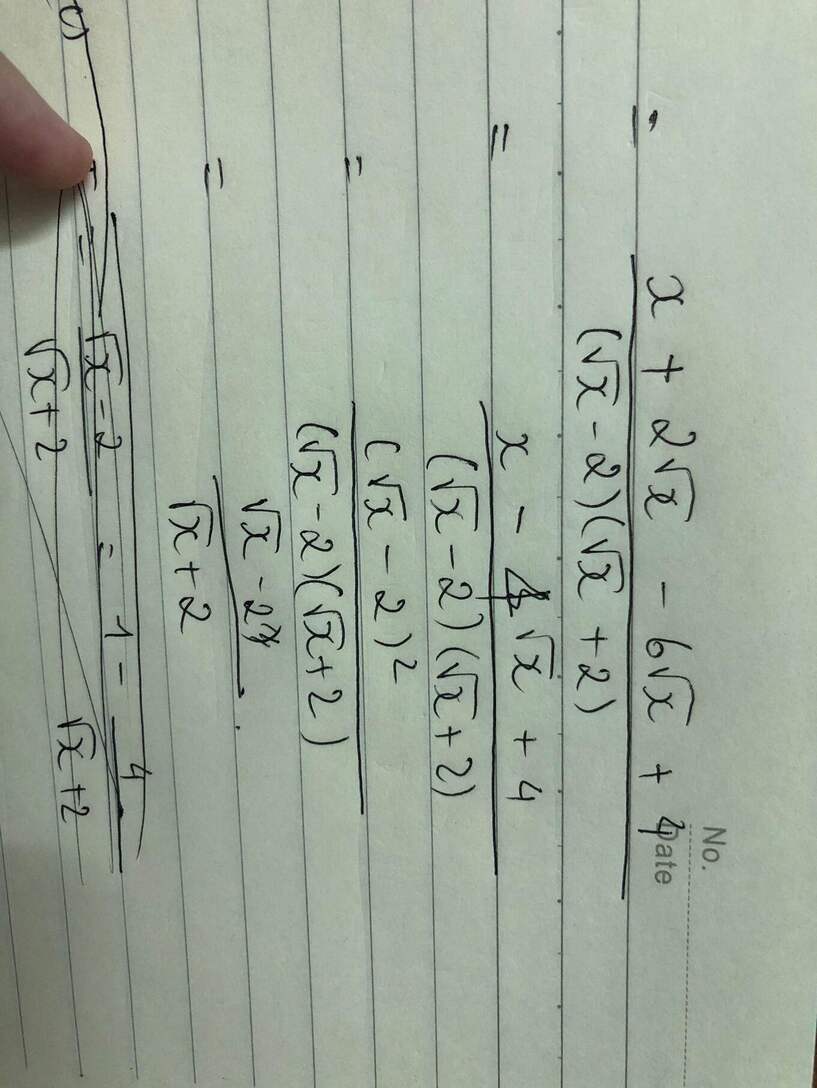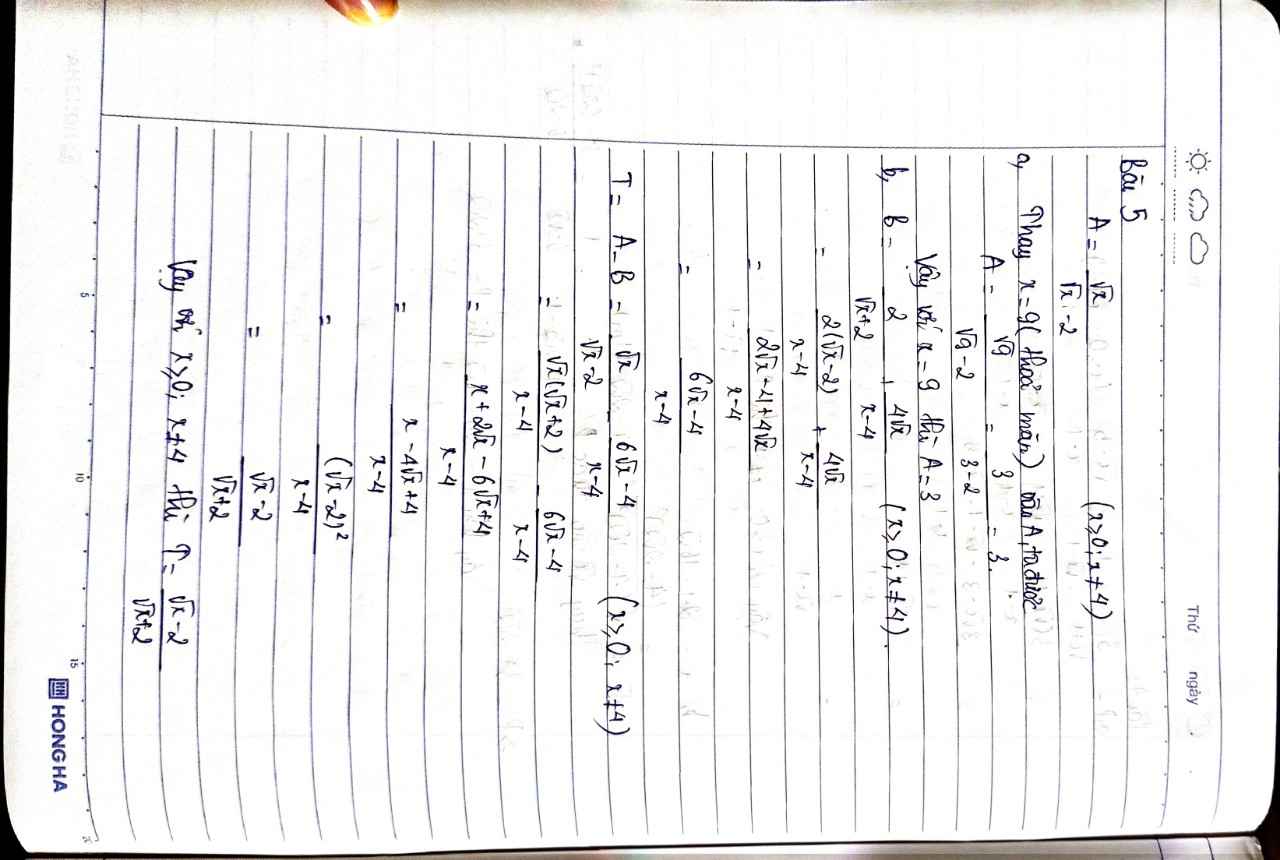Question

(Đề thi tuyển sinh vào 10 - Bình Định)

Cho biểu thức \(A=\dfrac{\sqrt{x}}{\sqrt{x}-2}\) và \(B=\dfrac{2}{\sqrt{x}+2}+\dfrac{4\sqrt{x}}{x-4}\).

a) Tính $A$ khi $x = 9$.

b) Thu gọn $T = A - B$.

c) Tìm $x$ nguyên để $T$ nguyên.

Answer 1

Trả lời:

a) Tính A khi x=9

Với x=9, A= \(\frac{\sqrt{9}}{\sqrt{9}-2}\)=3

b) Rút gọn:

T=A-B

T=\(\frac{\sqrt{x}}{\sqrt{x}-2}\)-\(\frac{2}{\sqrt{x}+2}\)-\(\frac{4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)

T=\(\frac{x-4\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)

T=\(\frac{\sqrt{x}-2}{\sqrt{x}+2}\)

c) Tìm x để T nguyên

T=\(\frac{\sqrt{x}-2}{\sqrt{x}+2}\)= 1-\(\frac{4}{\sqrt{x}+2}\)

T nguyên khi: 4 mod (\(\sqrt{x}\)+2)=0

=> \(\sqrt{x}+2\)={4,2,1}

=> \(\sqrt{x}\) ={2,0}

=> x={4,0}

Answer 2

Sao bài của mình làm khi post lên olm bị mất phần sau rồi ???

Answer 3

c) Tìm x để T nguyên:

T=1-\(\frac{4}{\sqrt{x}+2}\)

T nguyên => 4 mod (\(\left(\sqrt{x}+2\right)\)=0

=>\(\left(\sqrt{x}+2\right)\)={4,2,1} 

=>\(\sqrt{x}\) ={0} (loại nghiệm \(\sqrt{x}\)=2 và \(\sqrt{x}\)=-1)

=> x=0

Answer 4

Điều kiện: $x\ne 4,$ $x\ge 0$.

b) T=A−B=√x√x−2 −2√x+2 −4√xx−4 

=√x−2√x+2 .

c) Chú ý rằng:√x−2√x+2 =√x+2−4√x+2 =√x+2√x+2 −4√x+2 =1−4√x+2 

Vậy để $T$ nguyên thì 

Đáp số: $x=0$.

 Câu hỏi thuộc chủ đề: Rút gọn biểu thức chứa căn bậc hai

o l m . v n

Answer 5

a, A= 3

b, T= \(\dfrac{\sqrt{X}-2}{\sqrt{x}+2}\)

c, x>4

Answer 6

A=\(\dfrac{3}{7}\)

T=\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

x=0

Answer 7

Answer 8

a, A=3 khi x=9                                                                                                     b,T=\(\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\) với x\(\ge0\) ; x\(\ne4\)                                                                             c, Để T nguyên khi x\(\in\left\{1;9;0;16;36\right\}\)

Answer 9

a/ Thay x=9 ( TMDK) vào biểu thức A

⇒A=\(\dfrac{\sqrt{9}}{\sqrt{9}-2}=\dfrac{3}{3-2}=3\)

 Vậy A=3 khi x=9

b/    ĐKXD: x≠4 , x≥0

Ta có T=A-B

           ⇒T=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}+\dfrac{4\sqrt{x}}{x-4}\)=\(\dfrac{x+2\sqrt{x}-2\sqrt{x}+4}{\left(\sqrt{x}+2\right).\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+2\right)^2}{\left(\sqrt{x}+2\right).\left(\sqrt{x}-2\right)}\) 

              T=\(\dfrac{\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)}\)

   Vậy T=\(\dfrac{\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)}\) với x≠4,x≥0

c/ ĐKXD x≠4,x≥0

         Ta có T=\(\dfrac{\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)}\) = \(1+\dfrac{4}{\sqrt{x}-2}\)

     Để \(1+\dfrac{4}{\sqrt{x}-2}\)ϵ Z mà 1 ϵ Z⇒\(\dfrac{\text{​​}4}{\sqrt{x}-2}\) ϵ Z⇒\(\sqrt{x}-2\)⋮ 4⇒\(\sqrt{x}-2\)ϵ Ư₍₄₎

    Ta có bảng giá trị 

\(\sqrt{x}-2\)	-1	1	-2	2
x	1	9	0	16

           mà x≠4,x≥0

    Vậy x ϵ {0;1;9;16} thì P ϵ Z 

Answer 10

a)A=3 khi x=9

b) T=\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

c) x=0 thì T nguyên

Answer 11

a, Thay x=9 vào bt A, ta có 

A= 3

b, T  = \(\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x+2}\right)\left(\sqrt{x}-2\right)}\)

    T  = \(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

c,  Để T nguyên, ta có :

T = \(1-\dfrac{4}{\sqrt{x}+2}\)

Vậy để T nguyên thì x=0

Answer 12

Với x ≥0;x≠4

⇒\(\sqrt{x}=3\)

Thay  \(\sqrt{x}=3\) vào A, ta có

A=\(\dfrac{3}{3-2}=3\)

Vậy A=3 khi x=9

b)     Với x ≥0;x≠4 , ta có

T=A-B

=\(\dfrac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-2)\times(\sqrt{x}+2)}-\dfrac{2\times(\sqrt{x}-2)}{(\sqrt{x}-2)\times(\sqrt{x}+2)}-\dfrac{4\sqrt{x}}{(\sqrt{x}-2)\times(\sqrt{x}+2)}\)

=\(\dfrac{x+2\sqrt{x}-2\sqrt{x}+4-4\sqrt{x}}{(\sqrt{x}-2)\times(\sqrt{x}+2)}\)

=\(\dfrac{x-4\sqrt{x}+4}{(\sqrt{x}-2)\times(\sqrt{x}+2)}\)

=\(\dfrac{(\sqrt{x}-2)^2}{(\sqrt{x}-2)\times(\sqrt{x}+2)}\)

=\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

Vậy với x≥0;x≠4, T =\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

c)     T =\(\dfrac{\sqrt{x}+2-4}{\sqrt{x}+2}\)=\(1-\dfrac{4}{\sqrt{x}+2}\)

Để T ϵ\(ℤ\)⇔\(\left\{{}\begin{matrix}1\inℤ\\\dfrac{4}{\sqrt{x}+2}\inℤ\end{matrix}\right.\)

⇔\(\dfrac{4}{\sqrt{x}+2}\inℤ\)

Do xϵZ , x\(\ge\)0 ,x≠4, ⇒\(\left[{}\begin{matrix}\sqrt{x}\in I\\\sqrt{x}\inℕ\end{matrix}\right.\)

Với \(\sqrt{x}\)ϵI ⇔\(\sqrt{x}+2\in I\)⇔\(\dfrac{4}{\sqrt{x}+2}\in I\left(loại\right)\)

Với \(\sqrt{x}\inℕ\Leftrightarrow\sqrt{x}+2\in N\Leftrightarrow\dfrac{4}{\sqrt{x}+2}\inℕ\)

⇔4⋮\(\sqrt{x}+2\)

⇔\(\sqrt{x}+2\in\left\{1;-1;2;-2;4;-4\right\}\)

⇔\(\sqrt{x}\left\{0;2\right\}\)(vì \(\sqrt{x}\)≥0∀x≠4)

⇔x\(\in\left\{0\right\}\)(vì x ≥0;x≠4)

Vậy với x =0 thì T nguyên

 

Answer 13

Answer 14

a) \(\dfrac{\sqrt{9}}{\sqrt{9}-2}\)=\(3\)

Answer 15

a) A= 2

b) x=0

Answer 16

 

Answer 17

 

Answer 18

Answer 19

Điều kiện \(x\ge0,x\ne4\)

a,x=9(thỏa mãn)

Thay x =9 vào A

A=\(\dfrac{\sqrt{9}}{\sqrt{9}-2}=3\)

Vậy với x =9 thì A=3

b,B=\(\dfrac{2\sqrt{x}-4+4\sqrt{x}}{\left(\sqrt{x}+2\right).\left(\sqrt{x}-2\right)}\)

B=\(\dfrac{6\sqrt{x}-4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)

T=A-B

T=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{6\sqrt{x}-4}{\left(\sqrt{x}+2\right).\left(\sqrt{x}-2\right)}\)

T=\(\dfrac{x+2\sqrt{x}-6\sqrt{x}+4}{\left(\sqrt{x}+2\right).\left(\sqrt{x}-2\right)}\)

T=\(\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)

T=\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

c,T=\(1-\dfrac{4}{\sqrt{x}+2}\)

Để T nguyên =>\(\sqrt{x}+2\)thuộc Ư(4)

\(\sqrt{x}+2\)thuộc {4,2,1}

x thuộc {4,0}

Answer 20

Answer 21

 

Answer 22

 

Answer 23

 

Answer 24

Đk: x\(\ne4,x\ge0\)

a) A=\(\dfrac{\sqrt{9}}{\sqrt{9}-2}=3\)

b) T= A-B=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{4\sqrt{x}}{x-4}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

c)\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2-4}{\sqrt{x}+2}=\dfrac{\sqrt{x+2}}{\sqrt{x}+2}-\dfrac{4}{\sqrt{x}+2}=1-\dfrac{4}{\sqrt{x}+2}\)

Vậy để $T$ nguyên thì \(\dfrac{4}{\sqrt{x}+2}\inℤ\)

Đáp số: $x=0$.

Answer 25

a) A=3

b) T=\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

c) x=0

Answer 26

Answer 27

   

 

Answer 28

 

 

 

Answer 29

Answer 30